
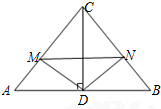
 如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB,M、N是AC、BC上的动点,且∠MDN=90°,下列结论正确的有( )个
如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB,M、N是AC、BC上的动点,且∠MDN=90°,下列结论正确的有( )个| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据等腰直角三角形的性质得出∠ADM=∠CDN;由ASA证明△AMD≌△CND,得出AM=CN,(1)正确;
证出CM=BN,根据勾股定理得出(2)正确;
四边形MDNC的面积=S△CDM+S△CDN=S△CDM+S△ADM=S△ADC.得出(3)正确;
当MN∥AB时,MN平分∠CND.得出(4)不正确.
解答 解:∵∠ACB=90°,AC=BC,CD⊥AB,
∴∠ADC=∠BDC=90°,AD=BD=CD=$\frac{1}{2}$AB,∠ACD=∠BCD=∠A=∠B=45°.
∵∠MDN=90°,
∴∠ADM=∠CDN.
在△AMD和△CND中,$\left\{\begin{array}{l}{A=∠DCN}&{\;}\\{AD=CD}&{\;}\\{∠ADM=∠CDN}&{\;}\end{array}\right.$,
∴△AMD≌△CND(ASA),
∴AM=CN,DM=DN,S△AMD=S△CND.
∴CM=BN.
∵四边形MDNC的面积=S△CDM+S△CDN=S△CDM+S△ADM=S△ADC.
∴四边形MDNC的面积是定值;
∵CM2+CN2=MN2,
∴BN2+AM2=MN2.
当MN∥AB时,MN平分∠CND.
∴正确的有:①②③;
故选:B.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定及性质、三角形的面积的计算;熟练掌握等腰直角三角形的性质和证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
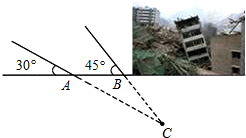 2015年4月25日14时11分,尼泊尔发生8.1级地震,震源深度20千米.中国救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
2015年4月25日14时11分,尼泊尔发生8.1级地震,震源深度20千米.中国救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知△ACD与△AGF都为等腰直角三角形,∠GAF=∠CAD=90°.连接GD、CF,N为线段GD的中点,连接AN.
已知△ACD与△AGF都为等腰直角三角形,∠GAF=∠CAD=90°.连接GD、CF,N为线段GD的中点,连接AN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com