
【题目】如图,一次函数y=kx+b与反比例函数 ![]() 的图像相交于A(2,3),B(﹣3,n)两点.
的图像相交于A(2,3),B(﹣3,n)两点. 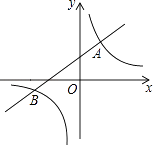
(1)求一次函数与反比例函数的解析式.
(2)根据所给条件,请直接写出不等式kx+b> ![]() 的解集.
的解集.
(3)连接OA、OB,求S△ABO .
【答案】
(1)解:∵反比例函数 ![]() 的图像经过A(2,3),
的图像经过A(2,3),
∴m=2×3=6,
∴反比例函数的解析式为:y= ![]() ,
,
∵反比例函数 ![]() 的图像经过于B(﹣3,n),
的图像经过于B(﹣3,n),
∴n= ![]() =﹣2,
=﹣2,
∴点B的坐标(﹣3,﹣2),
由题意得, ![]() ,
,
解得, ![]() ,
,
∴一次函数的解析式为:y=x+1
(2)解:由图像可知,不等式kx+b> ![]() 的解集为:﹣3<x<0或x>2
的解集为:﹣3<x<0或x>2

(3)解:直线y=x+1与x轴的交点C的坐标为(﹣1,0),
则OC=1,
则S△ABO=S△OBC+S△ACO= ![]() ×1×2+
×1×2+ ![]() ×1×3=
×1×3= ![]()
【解析】(1)根据反比例函数图像上点的坐标特征求出m和n,利用待定系数法求出一次函数的解析式;(2)根据函数图像得到答案;(3)求出直线与x轴的交点坐标,根据三角形的面积公式计算即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】市实验中学学生步行到郊外旅行.高一(1)班学生组成前队,步行速度为4千米/时,高一(2)班学生组成后队,速度为6千米/时.前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时.
(1)后队追上前队需要多长时间?
(2)后队追上前队时间内,联络员走的路程是多少?
(3)两队何时相距2千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
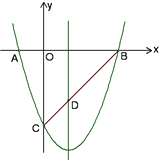
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ ![]() 时,求tan∠CED的值;
时,求tan∠CED的值;
②当以C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
(参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是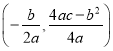 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要得到△ABD≌△ACD,还需从下列条件中补选一个,则错误的选法是( ) 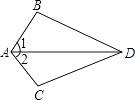
A.AB=AC
B.DB=DC
C.∠ADB=∠ADC
D.∠B=∠C
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com