
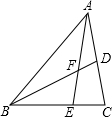
 如图,在△ABC中,D、E分别为AC、BC边上一点,AE与BD交于点F.已知AD=CD,BE=2CE,且△ABC的面积为60平方厘米,则△ADF的面积为6平方厘米;如果把“BE=2CE”改为“BE=nCE”其余条件不变,则△ADF的面积为$\frac{30}{2n+1}$平方厘米(用含n的代数式表示).
如图,在△ABC中,D、E分别为AC、BC边上一点,AE与BD交于点F.已知AD=CD,BE=2CE,且△ABC的面积为60平方厘米,则△ADF的面积为6平方厘米;如果把“BE=2CE”改为“BE=nCE”其余条件不变,则△ADF的面积为$\frac{30}{2n+1}$平方厘米(用含n的代数式表示). 分析 先连接CF,过点E作EG∥AC,交BD于G,根据平行线分线段成比例定理,得出$\frac{GE}{DC}$=$\frac{BE}{BC}$=$\frac{2}{3}$,$\frac{EF}{AF}$=$\frac{GE}{AD}$=$\frac{2}{3}$,再根据BE=2CE,且△ABC的面积为60平方厘米,求得△ACE的面积,再根据$\frac{EF}{AF}$=$\frac{2}{3}$,以及AD=CD,求得△ADF的面积即可;如果把“BE=2CE”改为“BE=nCE”其余条件不变,可以运用相同的方法得出△ADF的面积.
解答 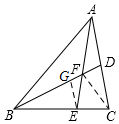 解:连接CF,过点E作EG∥AC,交BD于G,则
解:连接CF,过点E作EG∥AC,交BD于G,则
$\frac{GE}{DC}$=$\frac{BE}{BC}$=$\frac{2}{3}$,
∵AD=CD,
∴$\frac{GE}{AD}$=$\frac{2}{3}$,
又∵GE∥AD,
∴$\frac{EF}{AF}$=$\frac{GE}{AD}$=$\frac{2}{3}$,
∵BE=2CE,且△ABC的面积为60平方厘米,
∴△ACE的面积为60×$\frac{1}{3}$=20平方厘米,
∴△ACF的面积为20×$\frac{3}{5}$=12平方厘米,
∵AD=CD,
∴△ADF的面积=6平方厘米;
∵EG∥AC,
∴$\frac{GE}{DC}$=$\frac{BE}{BC}$=$\frac{n}{n+1}$,
∵AD=CD,
∴$\frac{GE}{AD}$=$\frac{n}{n+1}$,
又∵GE∥AD,
∴$\frac{EF}{AF}$=$\frac{GE}{AD}$=$\frac{n}{n+1}$,
∵BE=nCE,且△ABC的面积为60平方厘米,
∴△ACE的面积为60×$\frac{1}{n+1}$=$\frac{60}{n+1}$平方厘米,
∴△ACF的面积为$\frac{60}{n+1}$×$\frac{n+1}{2n+1}$=$\frac{60}{2n+1}$平方厘米,
∵AD=CD,
∴△ADF的面积=$\frac{30}{2n+1}$平方厘米;
故答案为:6,$\frac{30}{2n+1}$.
点评 本题主要考查了三角形的面积的计算,解决问题的关键是作平行线,根据平行线分线段成比例定理求得线段的比值.解题时注意:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
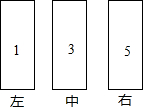 如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )
如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )| A. | 同样的音“1” | B. | 同样的音“3” | C. | 同样的音“5” | D. | 不同的两个音 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD为⊙O的内接四边形,对边BC,AD交于点F,AB、DC交于点E,△ECF的外接圆与⊙O的另一交点为H,AH与EF交于点M,MC与⊙O交于点C.证明:
如图,四边形ABCD为⊙O的内接四边形,对边BC,AD交于点F,AB、DC交于点E,△ECF的外接圆与⊙O的另一交点为H,AH与EF交于点M,MC与⊙O交于点C.证明:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
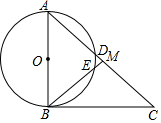 如图,在直角△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
如图,在直角△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com