
【题目】如图,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.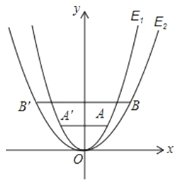
(1)求m的值;
(2)求抛物线E2所表示的二次函数的表达式;
(3)在第一象限内,抛物线E1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】解:(1)∵抛物线E1经过点A(1,m)
∴m=12=1
(2)∵抛物线E2的顶点在原点,可设它对应的函数表达式为y=ax2(a≠0)
又∵点B(2,2)在抛物线E2上
∴2=a×22 , 解得:a=![]()
∴抛物线E2所对应的二次函数表达式为y=![]() x2
x2
(3)如图所示: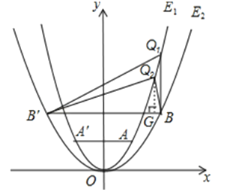
①当点B为直角顶点时,过B作Q1B⊥BB′交抛物线E1于Q,则点Q1与B的横坐标相等且为2,将x=2代入y=x2得y=4,
∴点Q1的坐标为(2,4).
②当点Q2为直角顶点时,则有Q2B′2+Q2B2=B′B2 , 过点Q2作GQ2⊥BB′于G,设点Q2的坐标为(t,t2)(t>0),则有(t+2)2+(t2﹣2)2+(2﹣t)2+(t2﹣2)2=4,
整理得:t4﹣3t2=0,
∵t>0,
∴t2﹣3=0,解得t1=![]() ,t2=﹣
,t2=﹣![]() (舍去),
(舍去),
∴点Q的坐标为(![]() ,3),
,3),
综上所述,存在符合条件的点Q坐标为(2,4)与(![]() ,3).
,3).
【解析】(1)将A(1,m)代入y=x2 , 求得m的值即可;
(2)设抛物线E2的函数表达式为y=ax2(a≠0),将点B(2,2)代入抛物线的解析式求得a的值即可;
(3)当∠BB′Q=90°时,将x=2代入y=x2 , 可求得点Q的纵坐标,当∠BQB′=90°时,设点Q2的坐标为(t,t2),依据两点间的距离公式和勾股定理的逆定理列出关于t的方程求解即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:
①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE ,
其中正确结论有( )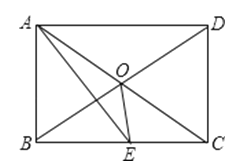
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
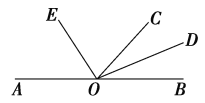
【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
(1)OD与OE的位置关系是______;(2)∠EOC的余角是_______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上的一点,OC为任一射线,OD平分∠BOC,OE平分∠AOC.
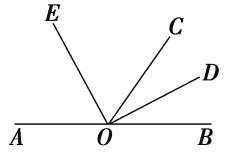
(1)指出图中∠AOD的补角和∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)3x+2(x2-y)-3(2x2+x-![]() y),其中x=
y),其中x=![]() ,y=-3;
,y=-3;
(2)3a2c-[2ab2-2(abc-![]() ab2)+3a2c]-abc,其中a=-
ab2)+3a2c]-abc,其中a=-![]() ,b=2,c=3.
,b=2,c=3.
查看答案和解析>>
科目:初中数学 来源: 题型:
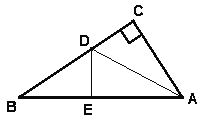
【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?若能,请给出求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组从![]() 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
![]() 求收工时,检修小组在
求收工时,检修小组在![]() 地的哪个方向?距离
地的哪个方向?距离![]() 地多远?
地多远?
![]() 在第几次纪录时距
在第几次纪录时距![]() 地最远?
地最远?
![]() 若汽车行驶每千米耗油
若汽车行驶每千米耗油![]() 升,问从
升,问从![]() 地出发,检修结束后再回到
地出发,检修结束后再回到![]() 地共耗油多少升?
地共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com