
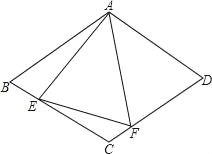
【题目】如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】试题分析:(1)先求证AB=AC,进而求证△ABC、△ACD为等边三角形,得∠4=60°,AC=AB进而求证△ABE≌△ACF,即可求得BE=CF;
(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题;
(3)当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又根据S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.
试题解析:(1)证明:连接AC,
∵∠1+∠2=60°,∠3+∠2=60°,
∴∠1=∠3,
∵∠BAD=120°,
∴∠ABC=∠ADC=60°
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∴△ABC、△ACD为等边三角形
∴∠4=60°,AC=AB,
∴在△ABE和△ACF中,
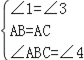 ,
,
∴△ABE≌△ACF.(ASA)
∴BE=CF.
(2)解:由(1)得△ABE≌△ACF,
则S△ABE=S△ACF.
故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,
是定值.
作AH⊥BC于H点,
则BH=2,
S四边形AECF=S△ABC
=![]()
=![]()
=![]() ;
;
(3)解:由“垂线段最短”可知,
当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的面积会随着AE的变化而变化,且当AE最短时,
正三角形AEF的面积会最小,
又S△CEF=S四边形AECF﹣S△AEF,则△CEF的面积就会最大.
由(2)得,S△CEF=S四边形AECF﹣S△AEF
=![]() ﹣
﹣![]() =
=![]() .
.


科目:初中数学 来源: 题型:
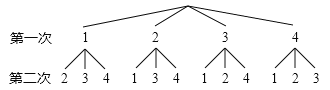
【题目】在不透明的袋子中有四张标着数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏.
小明画出树状图如图所示:
小华列出表格如下:

回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是,随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为 ;
(3)规定两次抽到的数字之和为奇数的获胜,你认为谁获胜的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲和乙同时从学校放学,两人以各自送度匀速步行回家,甲的家在学校的正西方向,乙的家在学校的正东方向,乙家离学校的距离比甲家离学校的距离远3900米,甲准备一回家就开始做什业,打开书包时发现错拿了乙的练习册.于是立即步去追乙,终于在途中追上了乙并交还了练习册,然后再以先前的速度步行回家,(甲在家中耽搁和交还作业的时间忽略不计)结果甲比乙晚回到家中,如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图,则甲的家和乙的家相距_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
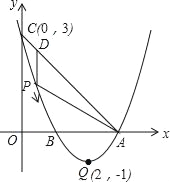
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100﹣90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
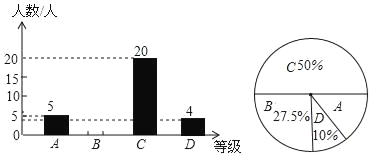
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
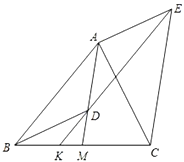
【题目】如图,![]() 是
是![]() 的中线,点
的中线,点![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 重合).过点
重合).过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)判断线段![]() 、
、![]() 的关系,并说明理由.
的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy 中,点A 的坐标为(1,0),P 是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).若点P到x轴的距离为![]() ,则m+n 的最小值为___.
,则m+n 的最小值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O直径,D为⊙O上一点,AT 平分∠BAD交⊙O于点 T,过 T 作AD的垂线交 A D的延长线于点 C。
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,CT=![]() ,求AD的长。
,求AD的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 两地相距1500米,甲、乙两人分别从
两地相距1500米,甲、乙两人分别从![]() 、
、![]() 两地同时出发,沿着同一条直线公路相向而行.若甲以7.5米/秒的速度骑自行车前进,乙以2.5米/秒的速度步行,甲出发1分钟后忘记带东西,迅速返回去取(掉头时间及取东西时间不计),则在乙出发经过__________秒两人相距100米.
两地同时出发,沿着同一条直线公路相向而行.若甲以7.5米/秒的速度骑自行车前进,乙以2.5米/秒的速度步行,甲出发1分钟后忘记带东西,迅速返回去取(掉头时间及取东西时间不计),则在乙出发经过__________秒两人相距100米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com