
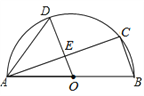
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.

(1)若∠B=70°,求弧CD的度数;
(2)若AB=26,DE=8,求AC的长.
【答案】(1)![]() 的度数是70°;(2) AC=24.
的度数是70°;(2) AC=24.
【解析】试题分析:(1)根据圆周角定理可得∠ACB=90°,则可得∠CAB的度数,由OD∥BC,可得∠AOD的度数,又OD=OA,从而可得∠OAD的度数,从而得到∠DAC的度数,继而得到弧CD的度数;
(2)易证OE是△ABC的中位线,由DE的长可得OE的长,利用中位线定理求得BC的长,由勾股定理即可得AC的长.
试题解析:(1)∵AB是直径,∴∠C=90°,∵∠B=70°,∴∠BAC=20°,
∵OD∥BC,∴∠AOD=∠B=70°,又OD=OA,∴∠OAD=55°,
∴∠DAC=35°,∴![]() 的度数是70°;
的度数是70°;
(2)∵AB=26,∴OD=13,又DE=8,∴OE=5,
∵OD∥BC,OA=OB,∴BC=2OE=10,又∵∠C=90°,∴AC=![]() =24.
=24.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△ABC沿x轴向左平移4个单位得到△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,并直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知长方形硬纸板ABCD的长BC为40cm,宽CD为30cm,按如图所示剪掉2个小正方形和2个小长方形(即图中阴影部分),将剩余部分折成一个有盖的长方体盒子,
设剪掉的小正方形边长为xcm.(纸板的厚度忽略不计)

(1)填空:EF= .cm,GH= .cm;(用含x的代数式表示)
(2)若折成的长方体盒子的表面积为950cm2,求该长方体盒子的体积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年,义乌市城市居民人均可支配收入约为44500元,居全省县级市之首,数字44500用科学记数法可表示为( )
A.4.45×103
B.4.45×104
C.4.45×105
D.4.45×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象经过点(-2,-4),且与正比例函数
的图象经过点(-2,-4),且与正比例函数![]() 的图象相交于点(4,a),求:
的图象相交于点(4,a),求:
(1)a的值;
(2)k、b的值;
(3)求出这两个函数的图象与y轴相交得到的三角形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com