
����Ŀ��7����ͼ1�ij�Ϊ![]() ����Ϊb
����Ϊb![]() ��С������ֽƬ������ͼ2��3�ķ�ʽ���ص��ط��� ����ABCD�ڣ�δ�����ǵIJ��֣��������Σ�����Ӱ��ʾ.
��С������ֽƬ������ͼ2��3�ķ�ʽ���ص��ط��� ����ABCD�ڣ�δ�����ǵIJ��֣��������Σ�����Ӱ��ʾ.
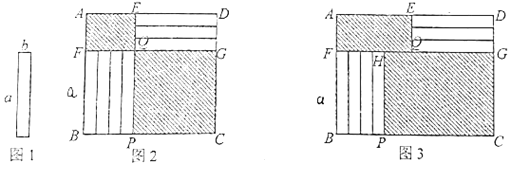
��1����ͼ2����E��Q��P��ͬһֱ���ϣ���F��Q��G��ͬһֱ���ϣ����½������Ͻǵ���Ӱ���ֵ�����IJ�Ϊ____________���ú�![]() ��
��![]() �Ĵ���ʽ��ʾ��������ABCD�����Ϊ____________���ú�
�Ĵ���ʽ��ʾ��������ABCD�����Ϊ____________���ú�![]() ��
��![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2����ͼ3����F��H��Q��G��ͬһֱ���ϣ������½������Ͻǵ���Ӱ���ֵ�����IJ�ΪS��![]() .
.
����![]() ��
��![]() ��
��![]() �Ĵ���ʽ��ʾAE��
�Ĵ���ʽ��ʾAE��
�ڵ�BC�ij��ȱ仯ʱ������ͬ���ķ��÷�ʽ��Sʼ�ձ��ֲ��䣬��ô![]() ��
��![]() ��������ʲô������
��������ʲô������
���𰸡���1��![]() ��
��![]() ��2��
��2��![]() ��
��![]()
��������
(1)���½ǵ�ͼ��Ϊ�߳�Ϊa�������Σ����Ͻ�ͼ��Ϊ�����Σ��䳤���ֱ�Ϊ4b��3b.�ֱ������������.�ҵ�����ABCD�ij����ֱ�Ϊa+4b��a+3b�����������.
(2) ��AE=FQ��PC=HG����FQ=HG+FH-QG���Ӷ��õ�AE.
�ڰ�S��ʾ������������˵���ʽΪ�㣬���ɵõ�S��BC������.
(1) ���½ǵ�ͼ��Ϊ�߳�Ϊa�������Σ����Ϊ![]() .
.
���Ͻ�ͼ��Ϊ�����Σ��䳤���ֱ�Ϊ4b��3b�����Ϊ![]() .
.
�����½������Ͻǵ���Ӱ���ֵ�����IJ�Ϊ![]() .
.
����ABCD�ij����ֱ�Ϊa+4b��a+3b�����Ϊ![]()
(2) �١�AE=FQ��PC=HG����FQ=HG+FH-QG
��AE=PC+FH-QG
��AE=x+4b-a
��ͼ2�У����½ǵľ��γ����ֱ�Ϊx��a�������Ϊxa.
���ϽǾ��γ����ֱ�Ϊx+4b-a��3b�������Ϊ3b��x+4b-a��.
��![]()
�����õ���![]()
��BC�ij��ȱ仯ʱ��Sʼ�ձ��ֲ��䣬��![]() ʱ����.
ʱ����.
�ʴ�Ϊ����1��![]() ��
��![]() ��2��
��2��![]() ��
��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ϵ�A��ʾ��a,��B��ʾ��b,��C��ʾ��c,a�Ƕ���ʽ2x24x+1��һ����ϵ��,b����С��������,����ʽ![]() x2y4�Ĵ���Ϊc.
x2y4�Ĵ���Ϊc.
![]()
(1)a=___��b=___��c=___��
(2)���������ڵ�B���۵�,���A���C___�غ�(��ܡ����ܡ�)��
(3)��A,B,C��ʼ���������˶�,����C��ÿ��1����λ���ȵ��ٶ������˶�,ͬʱ,��A�͵�B�ֱ���ÿ��3����λ���Ⱥ�2����λ���ȵ��ٶ������˹�,t���ӹ���,����A���B֮��ľ����ʾΪAB,��B���C֮��ľ����ʾΪBC,��AB=___,BC=___(�ú�t�Ĵ���ʽ��ʾ)��
(4)���ʣ�3ABBC��ֵ�Ƿ�����ʱ��t�ı仯���ı�?���仯����˵�����ɣ������䣬������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��E��F�ֱ���ABCD��AD��BC���ϵĵ㣬��AE=CF��

��1����֤����ABE�ա�CDF��
��2����M��N�ֱ���BE��DF���е㣬����MF��EN�����ж��ı���MFNE���������ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �ĶԽ���
�ĶԽ���![]() ��
��![]() ���ڵ�
���ڵ�![]() �������в����ж��ı���
�������в����ж��ı���![]() ��ƽ���ı��ε������ǣ� ��
��ƽ���ı��ε������ǣ� ��

A.![]() ��
��![]() ��
��![]()
B.��![]() =��
=��![]() ��
��![]() ��
��![]()
C.![]() ��
��![]() =
=![]()
D.��![]() =��
=��![]() ����
����![]() =��
=��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ƽ��ֱ������ϵ�У�������y=ax2+bx+3��x�����������ֱ�ΪA����3��0����B��1��0������y��Ľ���ΪD���Գ����������߽��ڵ�C����x�Ḻ���ύ�ڵ�H��
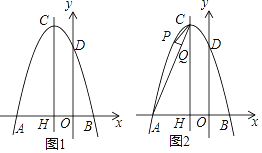
��1���������ߵı���ʽ��
��2����E��F�ֱ��������߶Գ���CH�ϵ��������㣨��E�ڵ�F�Ϸ�������EF=1����ʹ�ı���BDEF���ܳ���Сʱ�ĵ�E��F���꼰��Сֵ��
��3����ͼ2����PΪ�Գ�����࣬x���Ϸ����������ϵĵ㣬PQ��AC�ڵ�Q���Ƿ���������ĵ�Pʹ��PCQ����ACH���ƣ��������������P�����꣬����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijУ�ڴ��ư��ľ���е�ͳ�������ͼ1�Ǹ��꼶�������ռ�ܾ�������İٷֱȣ�ͼ2�ǶԲ���ѧ�������������ij������飮
��1���ڳ�ȡ�������У�������ƽ��������λ�����������Ƕ��٣�
��2������У���꼶����200�˾��������ȫУ�����ܽ��ԼΪ����Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB��AC����D�ڱ�BC���ڵ�ֱ���ϣ�����D��DF��AC��ֱ��AB�ڵ�F��DE��AB��ֱ��AC�ڵ�E�������ƽ���ı���AEDF��
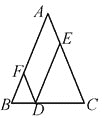
��1������D���߶�BC��ʱ�� ����֤��FB��FD������֤��DE��DF��AC��
��2����D�ڱ�BC���ڵ�ֱ���ϣ���AC��8��DE��3����������ʾ��ͼ��DF�ij��ȣ�����Ҫ֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������ӹ�A��������Ҹ���ӹ�B���������֪�ӹ�60��A���������ʱ����Ҽӹ�80��B���������ʱ����ͬ��ÿ��ס������˹��ӹ��������35�������ÿ��ӹ�x��A�������
��1����ס���ÿ����ӹ����ٸ������
��2�������г�Ԥ����ƣ��ӹ�һ��A���������õ�����Ϊ30Ԫ/�����ӹ�һ��B���������õ�����ÿ����A����5Ԫ��������Ҫ�ӹ��ס������������300����Ҫ������õ���������8250Ԫ��������Ӧ�������ٸ�A�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC��4����BAC��120����M��BC���е㣬��E��AB���ϵĶ��㣬��F���߶�BM�ϵĶ��㣬��ME+EF����Сֵ����____��
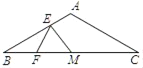
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com