
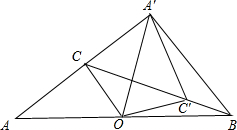
 如图,已知钝角三角形ABC,∠A=36°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,连接BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为18°.
如图,已知钝角三角形ABC,∠A=36°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,连接BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为18°. 分析 根据旋转的性质得出OA=OA′,∠OA′C′=∠A=36°,根据三角形外角的性质从而求得∠A′OB=72°,证得OA′=OB,根据等边对等角,得出∠OA′B=∠OBA′=54°,进而就可求得∠BA′C′=54°-36°=18°.
解答  解:如图,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,
解:如图,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,
则OA=OA′,∠OA′C′=∠A=36°,
∵点A、C、A′在同一直线上,连结CA′,
∴∠OA′A=∠A=36°,
∴∠A′OB=72°.
∵OC为边AB上的中线,
∴OA=OB,
∴OA′=OB,
∴∠OA′B=∠OBA′=54°,
∴∠BA′C′=54°-36°=18°.
故答案为18°.
点评 本题考查了旋转的性质,等腰三角形的判定和性质,三角形外角的性质,三角形的内角和定理,熟练掌握性质定理是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
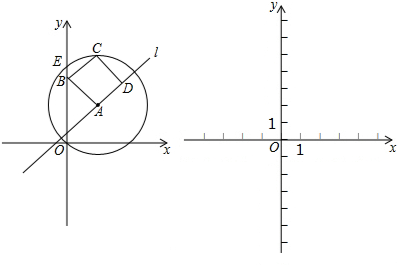
 如图,E(2,3),F(3,2)在正方形OABC的边上,⊙D分别切OE,OF于E,F,则⊙D的半径为$\frac{{\sqrt{13}}}{5}$.
如图,E(2,3),F(3,2)在正方形OABC的边上,⊙D分别切OE,OF于E,F,则⊙D的半径为$\frac{{\sqrt{13}}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
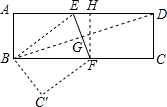 如图,矩形ABCD的长AD=9cm,宽AB=3cm,将它折叠,使点D与点B重合,求折叠后DE的长和EF的长分别是( )
如图,矩形ABCD的长AD=9cm,宽AB=3cm,将它折叠,使点D与点B重合,求折叠后DE的长和EF的长分别是( )| A. | 5cm,3cm | B. | 5cm,$\sqrt{10}$cm | C. | 6cm,$\sqrt{10}$cm | D. | 5cm,4cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1)2005=-1 | B. | |-3|=±3 | C. | ${({\frac{1}{3}})^{-1}}$=3 | D. | -22=-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4℃,4℃ | B. | 5℃,4℃ | C. | 4℃,3℃ | D. | 4℃,4.5℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,-1),并且与y轴交于点C(0,3),与x轴交于两点A,B.
如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,-1),并且与y轴交于点C(0,3),与x轴交于两点A,B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com