
【题目】在菱形ABCD中,∠BAD=60°.
(1)如图1,点E为线段AB的中点,连接DE,CE,若AB=4,求线段EC的长;
(2)如图2,M为线段AC上一点(M不与A,C重合),以AM为边,构造如图所示等边三角形AMN,线段MN与AD交于点G,连接NC,DM,Q为线段NC的中点,连接DQ,MQ,求证:DM=2DQ.

【答案】(1)2![]() (2)证明见解析
(2)证明见解析
【解析】试题分析:(1)如图1,连接对角线BD,先证明△ABD是等边三角形,根据E是AB的中点,由等腰三角形三线合一得:DE⊥AB,利用勾股定理依次求DE和EC的长;
(2)如图2,作辅助线,构建全等三角形,先证明△ADH是等边三角形,再由△AMN是等边三角形,得条件证明△ANH≌△AMD(SAS),则HN=DM,根据DQ是△CHN的中位线,得HN=2DQ,由等量代换可得结论.
试题解析:解:(1)如图1,连接BD,则BD平分∠ABC,∵四边形ABCD是菱形,∴AD∥BC,∴∠A+∠ABC=180°,∵∠A=60°,∴∠ABC=120°,∴∠ABD=![]() ∠ABC=60°,∴△ABD是等边三角形,∴BD=AD=4,∵E是AB的中点,∴DE⊥AB,由勾股定理得:DE=
∠ABC=60°,∴△ABD是等边三角形,∴BD=AD=4,∵E是AB的中点,∴DE⊥AB,由勾股定理得:DE=![]() =
=![]() ,∵DC∥AB,∴∠EDC=∠DEA=90°,在Rt△DEC中,DC=4,EC=
,∵DC∥AB,∴∠EDC=∠DEA=90°,在Rt△DEC中,DC=4,EC=![]() =
=![]() =
=![]() ;
;
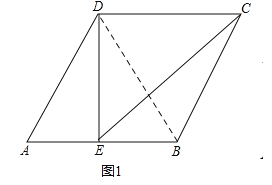
(2)如图2,延长CD至H,使CD=DH,连接NH、AH,∵AD=CD,∴AD=DH,∵CD∥AB,∴∠HDA=∠BAD=60°,∴△ADH是等边三角形,∴AH=AD,∠HAD=60°,∵△AMN是等边三角形,∴AM=AN,∠NAM=60°,∴∠HAN+∠NAG=∠NAG+∠DAM,∴∠HAN=∠DAM,在△ANH和△AMD中,∵AH=AD,∠HAN=∠DAM,AN=AM,∴△ANH≌△AMD(SAS),∴HN=DM,∵D是CH的中点,Q是NC的中点,∴DQ是△CHN的中位线,∴HN=2DQ,∴DM=2DQ.



科目:初中数学 来源: 题型:
【题目】某体育用品商店老板到体育商场批发篮球、足球、排球共![]() 个,得知该体育商场篮球、足球、排球平均每个
个,得知该体育商场篮球、足球、排球平均每个![]() 元,篮球比排球每个多
元,篮球比排球每个多![]() 元,排球比足球每个少
元,排球比足球每个少![]() 元.
元.
(1) 求出这三种球每个各多少元;
(2) 经决定,该老板批发了这三种球的任意两种共![]() 个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;
个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;
(3) 该老板打算将每一种球各提价![]() 元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由.
元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各式配成完全平方式:
①x2+6x+______=(x+____)2 ②x2-5x+_____=(x-____)2;
③x2+ x+______=(x+____)2 ④x2-9x+_____=(x-____)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明每天上午9时骑自行车离开家,15时回家,他描绘了离家的距与时间的变化情况.

(1)图象表示哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方时什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他由离家最远的地方返回的平均速度是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=![]() x-3与x轴,y轴分别交于点A和点B.
x-3与x轴,y轴分别交于点A和点B.
(1)求点A和点B的坐标;
(2)将直线l1向上平移6个单位后得到直线l2,求直线l2的函数解析式;
(3)设直线l2与x轴的交点为M,则△MAB的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC外角的平分线,已知∠BAC=∠ACD.
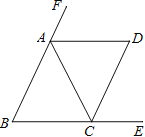
(1)求证:△ABC≌△CDA;
(2)若∠B=60°,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
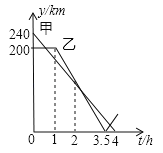
【题目】在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发![]() h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是______(填写所有正确结论的序号).
h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是______(填写所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA=OB=OC=6,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的![]() .
.
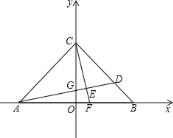
(1)求点D的坐标;
(2)过点C作CE⊥AD,交AB交于F,垂足为E.
①求证:OF=OG;
②求点F的坐标。
(3)在(2)的条件下,在第一象限内是否存在点P,使△CFP为等腰直角三角形?若存在,直接写出点P坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com