练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．如图，正方形网格中小正方形的边长都为1，请在此网格中作一个直角三角形，使三角形各边的长度都是无理数．

    分析 如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形，使a，b，c均为无理数即可．

    解答 解：如图所示，AC=BC=$\sqrt{10}$，AB=2$\sqrt{5}$，∠ACB=90°，故△ABC即为所求．

    点评 本题主要考查了勾股定理的逆定理以及无理数的运用，解题时注意：首先要理解题意，弄清问题中对所作图形的要求，结合对应几何图形的性质和基本作图的方法作图．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．计算
    （1）-12016+${（\frac{\sqrt{2-1}}{3}）}^{0}$-${（-\frac{1}{3}）}^{-1}$
    （2）（-2）3×$\sqrt{{（\frac{-3}{2}）}^{2}}$÷$\root{3}{-27}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．如图，在4×4正方形网格中，黑色部分的 图形构成一个轴对称图形，现在任意选取一个白色的小正方形并涂黑，使黑色部分的图形仍然构成一个轴对称图形的概率是（　　）
    A．$\frac{3}{13}$B．$\frac{4}{13}$C．$\frac{5}{13}$D．$\frac{6}{13}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

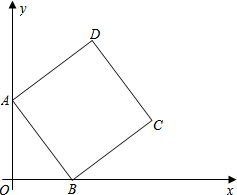    3．如图，在平面直角坐标系中，正方形ABCD的顶点A在y轴正半轴上，顶点B在x轴正半轴上，OA、OB的长满足（x-$\frac{7}{2}$）2=$\frac{1}{4}$中的x．其中OA＞OB．
    （1）求点D的坐标；
    （2）求直线BC的解析式；
    （3）在直线BC上是否存在点P，使△PCD为等腰三角形？若存在，请直接写出点P的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．“每天锻炼一小时，健康生活一辈子”，自开展“阳光体育运动”以来，学校师生的锻炼意识都增强了．某校有学生8200人，为了解学生每天的锻炼时间，学校体育组随机调查了部分学生，统计结果如表所示．
    表格中，m=30人；　这组数据的众数是14.5分钟；该校每天锻炼时间达到1小时的约有820人人．
    时间段频数频率
    29分钟及以下1080.54
    30-39分钟240.12
    40-49分钟m0.15
    50-59分钟180.09
    1小时及以上200.1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

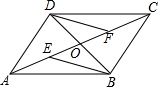    20．如图所示，四边形ABCD的对角线AC、BD交于点O，若OE=OF，DF∥BE．
    （1）求证：△BOE≌△DOF；
    （2）求证：四边形DEBF是平行四边形；
    （3）若OD=OE=OF，则四边形DEBF是什么特殊的四边形，请证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

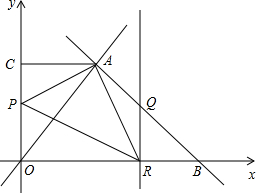    7．如图，已知直线y=-x+7与直线y=$\frac{4}{3}$x交于点A，且与x轴交于点B，过点A作AC⊥y轴与点C．点P从O点以每秒1个单位的速度沿折线O-C-A运动到A；点R从B点以相同的速度向O点运动，一个点到终点时，另一个点也随之停止运动．
    （1）求点A和点B的坐标；
    （2）过点R作直线l∥y轴，直线l交线段BA于点Q，设动点P运动的时间为t秒．
    ①当t为何值时，以A，P，O，R为顶点的四边形的面积为13？
    ②是否存在以A、P、R为顶点的三角形是等腰三角形？若存在，直接写出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，△ABC是直角三角形，∠ACB=90°，∠B=30°，以点C为旋转中心，将△ABC旋转到△A′B′C′的位置，且使A′B′经过点A．
    （1）求∠ACA′的度数，判断△ACA′的形状；
    （2）求线段AC与线段AB的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．一元二次方程x2-2$\sqrt{2}$x+m=0有一个实数根是$\sqrt{2}$+$\sqrt{3}$，则m的值为-1．

    查看答案和解析>>

    同步练习册答案