
【题目】在正方形ABCD中,E是CD边上的点,过点E作EF⊥BD于F.
(1)尺规作图:在图中求作点E,使得EF=EC;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接FC,求∠BCF的度数.

科目:初中数学 来源: 题型:
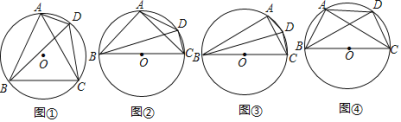
【题目】(1)方法选择
如图①,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() ,
,![]() .求证:
.求证:![]() .
.
小颖认为可用截长法证明:在![]() 上截取
上截取![]() ,连接
,连接![]() …
…
小军认为可用补短法证明:延长![]() 至点
至点![]() ,使得
,使得![]() …
…
请你选择一种方法证明.
(2)类比探究
(探究1)
如图②,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() .试用等式表示线段
.试用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
(探究2)
如图③,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() .若
.若![]() 是
是![]() 的直径,
的直径,![]() ,则线段
,则线段![]() ,
,![]() ,
,![]() 之间的等量关系式是______.
之间的等量关系式是______.
(3)拓展猜想
如图④,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() .若
.若![]() 是
是![]() 的直径,
的直径,![]() ,则线段
,则线段![]() ,
,![]() ,
,![]() 之间的等量关系式是______.
之间的等量关系式是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
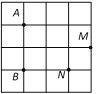
【题目】如图,在![]() 的正方形网格中,点A,B,M,N都在格点上.从点M,N中任取一点,与点A,B顺次连接组成一个三角形,则下列事件是必然事件的是( )
的正方形网格中,点A,B,M,N都在格点上.从点M,N中任取一点,与点A,B顺次连接组成一个三角形,则下列事件是必然事件的是( )
A.所得三角形是锐角三角形B.所得三角形是直角三角形
C.所得三角形是钝角三角形D.所得三角形是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() .
.
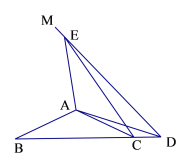
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,直接写出
的延长线上时,直接写出![]() 的度数;
的度数;
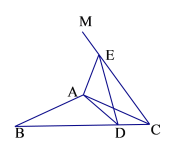
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 于点
于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y1=kx2+ax+a的图象与x轴交于点A,B(点A在点B的左侧),函数y2=kx2+bx+b,的图象与x轴交于点C,D(点C在点D的左侧),其中k≠0,a≠b.
(1)求证:函数y1与y2的图象交点落在一条定直线上;
(2)若AB=CD,求a,b和k应满足的关系式;
(3)是否存在函数y1和y2,使得B,C为线段AD的三等分点?若存在,求![]() 的值,若不存在,说明理由
的值,若不存在,说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[提出问题]正多边形内任意一点到各边距离之和与这个正多边形的边及内角有什么关系?
[探索发现]
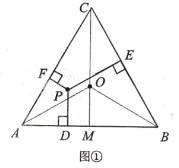
![]() 为了解决这个问题,我们不妨从最简单的正多边形-------正三角形入手
为了解决这个问题,我们不妨从最简单的正多边形-------正三角形入手
如图①,![]() 是正三角形,边长是
是正三角形,边长是![]() 是
是![]() 内任意一点,
内任意一点,![]() 到
到![]() 各边距离分别为
各边距离分别为![]() ,确定
,确定![]() 的值与
的值与![]() 的边及内角的关系.
的边及内角的关系.
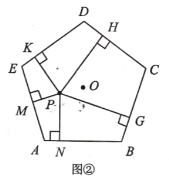
![]() 如图②,五边形
如图②,五边形![]() 是正五边形,边长是
是正五边形,边长是![]() 是正五边形
是正五边形![]() 内任意一点,
内任意一点,![]() 到五边形
到五边形![]() 各边距离分别为
各边距离分别为![]() , 参照
, 参照![]() 的探索过程,确定
的探索过程,确定![]() 的值与正五边形
的值与正五边形![]() 的边及内角的关系.
的边及内角的关系.
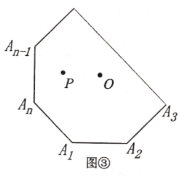
![]() 类比上述探索过程:
类比上述探索过程:
正六边形(边长为![]() )内任意一点
)内任意一点 ![]() 到各边距离之和
到各边距离之和![]()
正八边形(边长为![]() )内任意一点
)内任意一点![]() 到各边距离之和
到各边距离之和![]()
[问题解决]正![]() 边形(边长为
边形(边长为![]() )内任意-一点P到各边距离之和
)内任意-一点P到各边距离之和![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,圆内接四边形ABCD,AD=BC,AB是⊙O的直径.
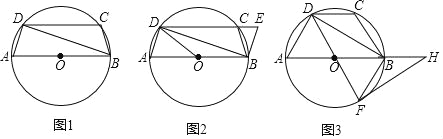
(1)求证:AB∥CD;
(2)如图2,连接OD,作∠CBE=2∠ABD,BE交DC的延长线于点E,若AB=6,AD=2,求CE的长;
(3)如图3,延长OB使得BH=OB,DF是⊙O的直径,连接FH,若BD=FH,求证:FH是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com