
【题目】如图,测得某楼梯的长为5m,高为3m,宽为2m,计划在表面铺地毯,若每平方米地毯50元,你能帮助算出至少需要多少钱吗?

【答案】至少需要700元.
【解析】
试题将每阶楼梯的横向线段和纵向线段分别向下和向右平移,则横向线段和纵向线段的和分别为直角三角形的两直角边长,根据勾股定理求得直角三角形下面直角边的长为4m,则楼梯表面所铺地毯是一个长为(4+3)m,宽为2m的长方形,据此即可计算出答案.
试题解析:
解:由勾股定理得:直角三角形下面直角边长为![]() =4m,
=4m,
将每阶楼梯的横向线段和纵向线段分别向下和向右平移,则横向线段和纵向线段的和分别为直角三角形的两直角边长,
∴地毯的长度为4+3=7(m),地毯的面积为:7×2=14(m2),
即:至少要购买地毯14平方米.
需要的费用为:14×50=700(元).
答:至少需要700元.


科目:初中数学 来源: 题型:
【题目】已知关于x的一次函数y=mx+2的图象经过点(﹣2,6).
(1)求m的值;
(2)画出此函数的图象;
(3)平移此函数的图象,使得它与两坐标轴所围成的图形的面积为4,请直接写出此时图象所对应的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接五一节,重百超市计划销售枇杷和樱桃两种水果共5000千克,若枇杷的数量是樱桃的2倍少1000千克.
(1)超市计划销售枇杷多少千克?
(2)若超市从某一果园直接进货,果园共30名员工负责采摘这两种水果,每人每天能够采摘30千克枇杷或10千克樱桃,应分别安排多少人采摘枇杷和樱桃,才能确保采摘两种水果所用的时间相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
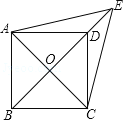
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m-3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第五个图形需要黑色棋子的个数是 ,第n个图形需要黑色棋子的个数是 (n≥1,且n为整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a ,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形.
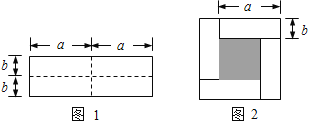
(1)图2的阴影部分的正方形的边长是 ______.
(2)用两种不同的方法求图中阴影部分的面积.
(方法1)![]() = _____________;
= _____________;
(方法2)![]() =______________;
=______________;
(3)观察如图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在梯形![]() 中,
中,![]() ,点
,点![]() 在直线
在直线![]() 上,联结
上,联结![]() ,过点
,过点![]() 作
作![]() 的垂线,交直线
的垂线,交直线![]() 与点
与点![]() ,
,



(1)如图1,已知![]() ,:求证:
,:求证:![]() ;
;
(2)已知:![]() ,
,
① 当点![]() 在线段
在线段![]() 上,求证:
上,求证:![]() ;
;
② 当点![]() 在射线
在射线![]() 上,①中的结论是否成立?如果成立,请写出证明过程;如果不成立,简述理由.
上,①中的结论是否成立?如果成立,请写出证明过程;如果不成立,简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
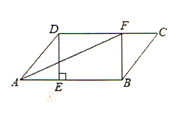
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com