
 已知:如图,在矩形ABCD中,E,F分别是AD,BC的中点,G,H分别是BE,DF的中点,连接EH和FG.
已知:如图,在矩形ABCD中,E,F分别是AD,BC的中点,G,H分别是BE,DF的中点,连接EH和FG.分析 (1)先连接EF,根据四边形ABFE、四边形CDEF都是矩形,得出GE=GF,EH=FH,再根据四边形DEBF是平行四边形,得出BE=DF,最后得到EG=GF=FH=EH,即可得出结论;
(2)根据有一个角是直角的菱形是正方形进行判断即可.
解答 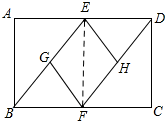 解:(1)连接EF,
解:(1)连接EF,
∵矩形ABCD中,AD=BC,E,F分别是AD,BC的中点,
∴AE=BF,
又∵AE∥BF,∠A=90°,
∴四边形ABFE是矩形,
∴∠BFE=90°,
∵G是BE的中点,
∴Rt△BEF中,GF=$\frac{1}{2}$BE=GE,①
同理可得,EH=$\frac{1}{2}$DF=FH,②
∵DE∥BF,DE=BF,
∴四边形DEBF是平行四边形,
∴BE=DF,③
由①②③可得,EG=GF=FH=EH,
∴四边形EGFH是菱形;
(2)当AB边和BC边之间满足条件:BC=2AB时,四边形EGFH是正方形.
理由:当AB边和BC边之间满足BC=2AB时,四边形ABFE与四边形CDEF都是正方形,
故∠GEF=∠HEF=45°,
∴∠GEH=90°,
∴菱形EGFH是正方形.
点评 本题主要考查了菱形的判定,矩形的判定与性质,正方形的判定的综合运用,解决问题的关键是作辅助线,构造矩形.解题时注意:先判定四边形是菱形,再判定这个矩形有一个角为直角,可得四边形为正方形.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,E为正方形ABCD的对角线BD上一点,△CEF为等腰直角三角形,连BF.若BD=4$\sqrt{2}$,则△BCF的面积为9.
如图所示,E为正方形ABCD的对角线BD上一点,△CEF为等腰直角三角形,连BF.若BD=4$\sqrt{2}$,则△BCF的面积为9.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 菱形ABCD在平面直角坐标系中的位置如图所示,其中A(1,0),B(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒2个单位长度的速度移动,当移动到第2016秒时,点P的坐标为(1,0).
菱形ABCD在平面直角坐标系中的位置如图所示,其中A(1,0),B(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒2个单位长度的速度移动,当移动到第2016秒时,点P的坐标为(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
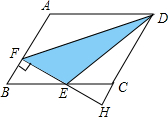 如图,在平行四边形ABCD中,E是BC中点,S四边形ABCD=24,AF=2FB,FE的延长线与DC的延长线相交于点H,则△DEF的面积是( )
如图,在平行四边形ABCD中,E是BC中点,S四边形ABCD=24,AF=2FB,FE的延长线与DC的延长线相交于点H,则△DEF的面积是( )| A. | 8 | B. | 16 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 某市政府位于北京路32号 | B. | 小明住在某小区3号楼7号 | ||
| C. | 太阳在我们的正上方 | D. | 东经130°,北纬54°的城市 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x<7与2x+$\sqrt{x}$<7+$\sqrt{x}$ | B. | (x+1)2>0,与x+1≠0 | ||
| C. | |x-3|>1与x-3>1 | D. | (x+1)3>x3与$\frac{1}{x+1}$<$\frac{1}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com