
分析 分别求得第1、2、3…12次变换后的坐标,得到每12次循环一次.则2015÷12=167…11,即可求得结果.
解答 解:由题意第1次旋转后的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
第2次旋转后的坐标为($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),
第3次旋转后的坐标为(0,1),
第4次旋转后的坐标为(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),
第5次旋转后的坐标为($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
第6次旋转后的坐标为(-1,0),
第7次旋转后的坐标为($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$),
第8次旋转后的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
第9次旋转后的坐标为(0,-1),
第10次旋转后的坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
第11次旋转后的坐标为(-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$),
第12次旋转后的坐标为(1,0),
每12次循环一次.
因为2015÷12=167…11,
所以把点A经过连续2015次这样的变换得到的点A2015的坐标是(-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
故答案是:(-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
点评 本题考查了坐标与图形变化-旋转.解答此类找规律的问题的关键是仔细分析题中所给的特征得到规律,再把这个规律应用于解题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
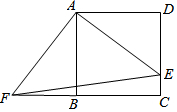 如图,四边形ABCD是正方形,E、F分别是边DC和CB延长线上的点,且DE=BF,连接AE,AF,EF
如图,四边形ABCD是正方形,E、F分别是边DC和CB延长线上的点,且DE=BF,连接AE,AF,EF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
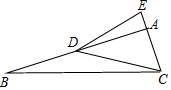 已知:如图,在△ABC中,∠BAC=90°,点D在AB上,点E在CA的延长线上,连接DC、DE,∠EDC=45°,BD=EC,DE=5$\sqrt{2}$,tan∠DCE=$\frac{3}{13}$,则CE=$\frac{5\sqrt{18}}{3}$.
已知:如图,在△ABC中,∠BAC=90°,点D在AB上,点E在CA的延长线上,连接DC、DE,∠EDC=45°,BD=EC,DE=5$\sqrt{2}$,tan∠DCE=$\frac{3}{13}$,则CE=$\frac{5\sqrt{18}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com