
| A. | 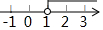 | B. | 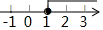 | C. | 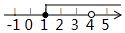 | D. | 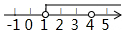 |
分析 首先根据解分式方程的方法,求出分式方程的解是多少;然后根据x≥0,求出a的取值范围即可.
解答 解:去分母,可得:2(2x-a)=x-2,
去括号,可得:4x-2a=x-2
移项,合并同类项,可得:3x=2a-2
解得x=$\frac{2a-2}{3}$,
经检验,x=$\frac{2a-2}{3}$是原方程的解,
∵x=$\frac{2a-2}{3}$≥0,
∴a≥1,
∵x-2≠0,
∴x≠2,
∴$\frac{2a-2}{3}$≠2,
解得a≠4,
∴a≥1且a≠4,
a的取值范围在数轴上表示为: .
.
故选:C.
点评 此题主要考查了分式方程的解,要熟练掌握,注意:在解方程的过程中因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根,增根是令分母等于0的值,不是原分式方程的解.


科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
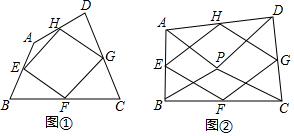
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
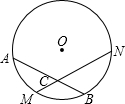 如图所示,M是弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4$\sqrt{3}$cm,则∠ACM的度数是( )
如图所示,M是弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4$\sqrt{3}$cm,则∠ACM的度数是( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
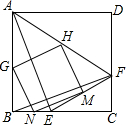 如图,在正方形ABCD中,点E,F分别在BC,CD边上,且BE=CF,连接AE,BF,EF、AF,点G、H、M、N分别是AB,AF,EF,BE的中点.
如图,在正方形ABCD中,点E,F分别在BC,CD边上,且BE=CF,连接AE,BF,EF、AF,点G、H、M、N分别是AB,AF,EF,BE的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②④ | C. | ②⑤ | D. | ③⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com