
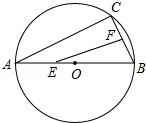
 如图,AB是⊙O的直径,弦AC=8cm,BC=6cm,若动点E以2cm/s的速度从A向B运动,点F以1cm/s的速度从B向C运动,设运动时间为t(s),连接EF,当△BEF是直角三角形时,求t(s)的值.
如图,AB是⊙O的直径,弦AC=8cm,BC=6cm,若动点E以2cm/s的速度从A向B运动,点F以1cm/s的速度从B向C运动,设运动时间为t(s),连接EF,当△BEF是直角三角形时,求t(s)的值. 分析 应分两种情况进行讨论,当EF⊥BC时,△BEF为直角三角形,根据△BEF∽△BAC,可将时间t求出;当EF⊥BA时,△BEF为直角三角形,根据△BEF∽△BCA,可将时间t求出.
解答 解:∵AB是⊙O的直径,弦AC=8cm,BC=6cm,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}=\sqrt{{8}^{2}+{6}^{2}}=10$,
根据题意得:BE=(10-2t)cm,BF=tcm;
如图(2),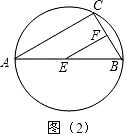
当EF⊥BC时,△BEF为直角三角形,
∴△BEF∽△BAC;
∴$\frac{BE}{BA}=\frac{BF}{BC}$,
即:$\frac{10-2t}{10}=\frac{t}{6}$,
解得:t=$\frac{30}{11}$;
如图(3),
当EF⊥BA时,△BEF为直角三角形,
∴△BEF∽△BCA,
∴$\frac{BE}{BC}=\frac{BF}{BA}$,
即:$\frac{10-2t}{6}=\frac{t}{10}$,
解得:t=$\frac{50}{13}$;
∴当t=$\frac{30}{11}$s或t=$\frac{50}{13}$s时,△BEF为直角三角形,.
点评 本题考查圆周角定理、相似三角形的性质、直角三角形的性质等知识的综合应用能力.解决本题的关键是在求时间t时应分情况进行讨论,防止漏解.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
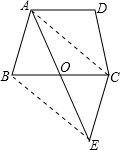 如图,梯形ABCD中,AD∥BC,AB=AD=DC,O是BC中点,将△ABO绕点O旋转180°至△ECO.
如图,梯形ABCD中,AD∥BC,AB=AD=DC,O是BC中点,将△ABO绕点O旋转180°至△ECO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
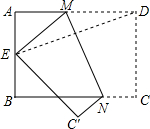 如图,四边形ABCD为矩形,AB=6,BC=8,E为AB的中点,将矩形ABCD折叠,使得点D与点E重合,折痕为MN,则折痕MN的长度为$\frac{3\sqrt{73}}{4}$.
如图,四边形ABCD为矩形,AB=6,BC=8,E为AB的中点,将矩形ABCD折叠,使得点D与点E重合,折痕为MN,则折痕MN的长度为$\frac{3\sqrt{73}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com