
����Ŀ����1����ͼ�٣��ı��� ABCD �������Σ��� G �� BC �ϵ�����һ�㣬BF AG �ڵ� F��DE AG�ڵ� E��̽�� BF��DE��EF ֮���������ϵ����һѧϰС�����̽���õ�DE�CBF= EF����֤��������ۣ�
��2������1���еĵ� G �� CB ���ӳ����ϣ������������䣬����ͼ���л���ͼ�Σ���ֱ��д����ʱ BF��DE��EF ֮���������ϵ��
��3����ͼ �� ���ı��� ABCD �ڽ��� ��O��AB=AD��E ��F ��AC �ϵ����㣬�������AED=��BFA=��BCD�����ж� AC��DE��BF ֮���������ϵ����˵�����ɣ�

���𰸡���1��֤������������2��EF=BF+DE����3��AC=BF+DE��֤��������
����������1����������ABCD��BF��AG��DE��AG
�� AB=AD��
��BAF+��DAE=��BAF+��ABF=��AFB=��DEA=900
���DAE=��ABF
���ADE�ա�BAF
��BF=AE��AF=DE
�� EF= AF �CAE = DE�C BF

��2����ͼ��ͼ��ʾ

EF=BF+DE
��3���� �ı���ABCD�ڽ���Բ
�� ��BCD+��BAD=1800
�� ��AED=��BCD����AED+��DEC=1800
���BAD=��DEC
�� ��BAD=��1+��2����DEC=��1+��3
���2=��3
�ߡ�AED=��BFA��AB=AD
�� ��ADE�ա�BAF
�� AE=BF��DE=AF
����BD
�ߡ�AED=��BCD����1=��DBC
���3=��4
���ADB=��EDC
��AB=AD
���ADB=��ABD=��ACD
�� ��EDC=��ACD
�� DE=CE=AF
�� AC=AE+CE=BF+DE




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=90�㣬OMƽ�֡�AOB����ֱ�����ǰ�Ķ���P������OM���ƶ�����ֱ�DZ߷ֱ���OA��OB�ཻ�ڵ�C��D����PC��PD�������˵�����ɣ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�Լ��ˮ��ij�о�������������ˮ�շѷ������涨��
�����ÿ��ÿ��ˮ������![]() �֣�ÿ��ˮ�շ�
�֣�ÿ��ˮ�շ�![]() Ԫ��
Ԫ��
�����ÿ��ÿ����ˮ����![]() �֣�������ÿ��ˮ�շ�
�֣�������ÿ��ˮ�շ�![]() Ԫ��
Ԫ��
С�쿴�������շѷ���������������ÿ�µ�ˮ�ѣ����������������ÿ�µ���ˮ�Ƿ�![]() �֣�
�֣�
��![]() �����С���ÿ����ˮ
�����С���ÿ����ˮ![]() �֣�ˮ���Ƕ��٣����ÿ����ˮ
�֣�ˮ���Ƕ��٣����ÿ����ˮ![]() �֣�ˮ���Ƕ��٣�
�֣�ˮ���Ƕ��٣�
��![]() �������ĸ
�������ĸ![]() ��ʾС���ÿ����ˮ�Ķ�������ôС���ÿ�µ�ˮ�Ѹ������
��ʾС���ÿ����ˮ�Ķ�������ôС���ÿ�µ�ˮ�Ѹ������![]() �Ĵ���ʽ��ʾ�أ�
�Ĵ���ʽ��ʾ�أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��
��֪����ʽA=3a2��6ab+b2 �� B=��2a2+3ab��5b2 �� ��a=1��b=��1ʱ������A+2B��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ѧУΪʹ��һ������У��ʱ���Ϻ�����У��������ǰ��ijУ���꼶����ѧ����������У���ͺ���������������飬�����ݵ���������������������������ͳ��ͼ��У���ͺ���������Ϊ��������Ϊ6���ͺţ�

����������Ϣ������������⣺
(1)�ð�ж�����ѧ�������д�175��У����ѧ���ж�������
(2)������ͳ��ͼ�У���ѿ�ȱ�IJ��ֲ���������
(3)������ͳ��ͼ�У������185��У������Ӧ����Բ�ĽǵĴ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��BDΪ��ABC�Ľ�ƽ���ߣ���BD=BC��EΪBD�ӳ����ϵ�һ�㣬BE=BA����E��EF��AB��FΪ���㣮���н��ۣ��١�ABD�ա�EBC���ڡ�BCE+��BCD=180�㣻��AD=AE=EC����BA+BC=2BF��������ȷ���ǣ� �� 
A.�٢ڢ�
B.�٢ۢ�
C.�٢ڢ�
D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�������У�50�����ݷֱ�����5�����ڣ���һ�����������ġ��������ݵĸ����ֱ�Ϊ2��8��15��20��5����������Ƶ��Ϊ�� ��
A. 0.1�� B. 0.2�� C. 0.3�� D. 0.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����dzߵ�ֱ�Ƕ���O�ص���һ��


��1����ͼ1����OCƽ�֡�AOB��������ʱOB�Dz���ƽ�֡�COD����_________(ֻ�ش���������������������)
��2����ͼ21��2������COB=��1��OB�ڡ�COD���ڲ�����������AOC���DOB�Ƿ���ȣ����������ɣ�
��3���ڣ�2���������£����ʡ�COB���AOD�ĺ��Ƕ��٣�����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
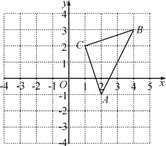
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�������ABC�Ķ��㶼�������ϣ�ƽ��������ABC��ʹ��C������ԭ��O�غϣ�
��1����д��ͼ�е�A��B��C�����ꣻ
��2������ƽ�ƺ��������OA1B1��
��3����������OA1A�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com