
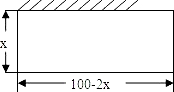
 才能符合要求呢?你能设计出最优方案吗?
才能符合要求呢?你能设计出最优方案吗?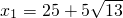 ,
,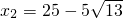 ,
,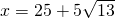 ,
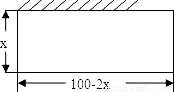
,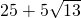 也是符合方案要求的一种设计,
也是符合方案要求的一种设计,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
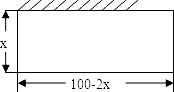 才能符合要求呢?你能设计出最优方案吗?
才能符合要求呢?你能设计出最优方案吗?查看答案和解析>>
科目:初中数学 来源: 题型:
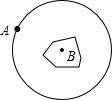 如图,有一个直径为100m的圆形湖泊,岸边有一个小木柱A,湖中央有一小岛,在小岛的中心打下小木柱B.一个人不会游泳,但他有一条绳子,这条绳子比100m长一些,用什么方式他能利用绳子和小木柱横渡到小岛上?
如图,有一个直径为100m的圆形湖泊,岸边有一个小木柱A,湖中央有一小岛,在小岛的中心打下小木柱B.一个人不会游泳,但他有一条绳子,这条绳子比100m长一些,用什么方式他能利用绳子和小木柱横渡到小岛上?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
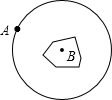 如图,有一个直径为100m的圆形湖泊,岸边有一个小木柱A,湖中央有一小岛,在小岛的中心打下小木柱B.一个人不会游泳,但他有一条绳子,这条绳子比100m长一些,用什么方式他能利用绳子和小木柱横渡到小岛上?
如图,有一个直径为100m的圆形湖泊,岸边有一个小木柱A,湖中央有一小岛,在小岛的中心打下小木柱B.一个人不会游泳,但他有一条绳子,这条绳子比100m长一些,用什么方式他能利用绳子和小木柱横渡到小岛上?查看答案和解析>>
科目:初中数学 来源:2008-2009学年江苏省无锡市江阴市周庄中学九年级(上)第一次段考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com