
分析 (1)根据偶次方及绝对值的非负性即可得出b、c的值,再根据五次四项式的定义即可求出a值;
(2)①根据点P、Q的运动,找出点P、Q代表的数,令其相等即可得出关于t的一元一次方程,解方程即可得出结论;
②设P运动(x+1.5)秒后这两点之间的距离为2个单位,则此时点P表示的数为2x-3,点Q表示的数为24-3x,根据两点间的距离公式即可得出关于x的含绝对值符号的一元一次方程,解方程即可得出x的值,再加上1.5即可得出结论.
解答 解:(1)∵(b+3)2+|c-24|=0,
∴b+3=0,c-24=0,
∴b=-3,c=24.
∵多项式x|a+3|y2-ax3y+xy2-1是五次四项式,
∴|a+3|+2=5,且a≠0,
解得:a=-6.
故答案为:-6;-3;24.
(2)①t秒后,点P表示的数为2t-6,点Q表示的数为24-3t,
∵t秒后点P和点Q相遇在点D,
∴2t-6=24-3t,
解得:t=6,
2t-6=6,
∴t的值为6,点D所表示的数为6.
②设P运动(x+1.5)秒后这两点之间的距离为2个单位,则此时点P表示的数为2x-3,点Q表示的数为24-3x,
根据题意得:|24-3x-(2x-3)|=2,
解得:x1=5,x2=5.8,
∴x+1.5=6.5或7.3.
答:P运动6.5秒或7.3秒后这两点之间的距离为2个单位.
点评 本题考查了偶次方及绝对值的非负性、多项式、数轴以及一元一次方程的应用,根据点与点之间的关系列出一元一次方程是解题的关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
 如图所示,在平面直角坐标系中,点B的坐标是(-1,0),点C的坐标是(1,0),点D为y轴上一点,点A为第二象限内一动点,且∠BAC=2∠BDO,过D作DM⊥AC于点M.
如图所示,在平面直角坐标系中,点B的坐标是(-1,0),点C的坐标是(1,0),点D为y轴上一点,点A为第二象限内一动点,且∠BAC=2∠BDO,过D作DM⊥AC于点M.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 个 | B. | 1 个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
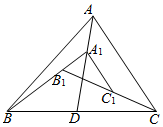 如图,在△ABC中,BD=DC,AA1=$\frac{1}{3}$AD,A1B1=$\frac{1}{3}$A1B,B1C1=C1C,△A1B1C1面积为1平方厘米,则△ABC的面积为多少平方厘米?
如图,在△ABC中,BD=DC,AA1=$\frac{1}{3}$AD,A1B1=$\frac{1}{3}$A1B,B1C1=C1C,△A1B1C1面积为1平方厘米,则△ABC的面积为多少平方厘米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com