练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
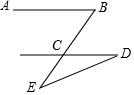
    14．如图，AB∥CD，E是BC延长线上一点，若∠B=50°，∠D=20°，则∠E的度数为（　　）
    A．20°B．30°C．40°D．50°

    分析 根据平行线的性质，得出∠BCD=∠B=50°，再根据∠BCD是△CDE的外角，即可得出∠E．

    解答 解：∵AB∥CD，
    ∴∠BCD=∠B=50°，
    又∵∠BCD是△CDE的外角，
    ∴∠E=∠BCD-∠D=50°-20°=30°．
    故选：B．

    点评 本题主要考查了平行线的性质以及三角形外角性质的运用，解题时注意：两直线平行，内错角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    4．矩形具有而菱形不一定具有的性质是（　　）
    A．对角线互相垂直B．对角线相等C．对角线互相平分D．对角相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，直线y=$\frac{3}{4}$x+3与x轴交于点C，与y轴交于点B，抛物线y=ax2-$\frac{3}{4}$x+c经过B、C两点．
    （1）求抛物线的解析式；
    （2）如图1，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标和△BEC面积的最大值；
    （3）如图2，抛物线的顶点为D，对称轴交直线BC于点N，设P为直线BC上动点，过点P作PF∥ND，交BC上方抛物线于点F，问在直线BC上是否存在一点P，使以P，F，D，N为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．如图，香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合，则n的最小值为（　　）
    A．45B．60C．72D．144

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列选项中，左边的平面图形能够折成右边封闭的立体图形的是（　　）
    A．B．
    C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

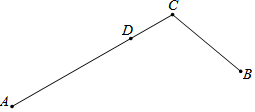    1．如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分，这点叫做这条折线的“折中点”．如图，点D是折线A-C-B的“折中点”，请解答以下问题：
    （1）当AC＞BC时，点D在线段AC上；
    当AC=BC时，点D与C重合；
    当AC＜BC时，点D在线段BC上；
    （2）若AC=18cm，BC=10cm，若∠ACB=90°，有一动点P从C点出发，在线段CB上向点B运动，速度为2cm/s，设运动时间是t（s），求当t为何值，三角形PCD的面积为10cm2？
    （3）若E为线段AC中点，EC=8cm，CD=6cm，求CB的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．在平面直角坐标系中，O是坐标原点，过点A（8，6）分别作x轴和y轴的平行线，交y轴于点B，交x轴于点C，M是线段AB的中点，点P从M点出发沿线段MA-AC向终点C运动，速度为每秒个单位长度，设点P运动的时间为t（秒）．
    （1）请直接写出点B和点C的坐标：B（0，，6），C（8，0）；
    （2）用含有t的代数式表示线段AP的长度，并直接写出t的取值范围．
    （3）作线段OP、PM，当三角形MOP的面积等于直角梯形AMOC的面积的$\frac{1}{2}$时，求t的值，并求出此时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知：如图菱形ABCD中，∠BAD=120°，AC=4，则该菱形的面积是（　　）
    A．16$\sqrt{3}$B．16C．8$\sqrt{3}$D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．已知x+y=3，xy=1，则（1）x2y+xy2═3；（2）x2+y2=7．

    查看答案和解析>>

    同步练习册答案