
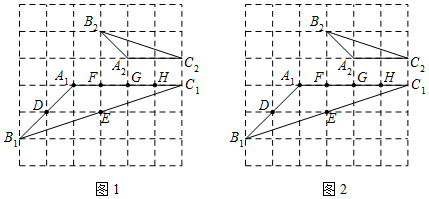
���� ��1��ֱ�����ù��ɶ����ó������θ��߳��������������������ε��ж������ʵó��𰸣�
��2���������������ε��ж������ó���������Ĵ𰸣�
��� �⣺��1����A1B1=2$\sqrt{2}$��A2B2=$\sqrt{2}$��A1C1=4��A2C2=2��
C2B2=$\sqrt{10}$��B1C1=2$\sqrt{10}$��
��$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=2��
���A1B1C1�ס�A2B2C2��
���A1B1C1�͡�A2B2C2�������Ϊ��4��1��
��2����ͼ2��ʾ����DEG����A1DG����A1DF����EGH�����A2B2C2���ƣ�
���� ������Ҫ���������Ʊ任����ȷ�������������ε��ж������ǽ���ؼ���


 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
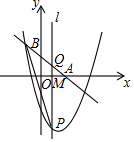 ��ͼ����ֱ֪��y=-$\frac{3}{4}$x+1�ֱ�x�ᡢy���ڵ�A��B��M��x����������һ���㣬����ÿ��1����λ���ٶȴ�O����x���������˶�������M��x��Ĵ���l����������y=x2-$\frac{5}{2}$x-2���ڵ�P����ֱ��AB���ڵ�Q������BP������t��ʱ����PBQ����BQΪ���ĵ��������Σ���t��ֵ��2��$\frac{3+\sqrt{21}}{2}$��$\frac{31}{8}$��
��ͼ����ֱ֪��y=-$\frac{3}{4}$x+1�ֱ�x�ᡢy���ڵ�A��B��M��x����������һ���㣬����ÿ��1����λ���ٶȴ�O����x���������˶�������M��x��Ĵ���l����������y=x2-$\frac{5}{2}$x-2���ڵ�P����ֱ��AB���ڵ�Q������BP������t��ʱ����PBQ����BQΪ���ĵ��������Σ���t��ֵ��2��$\frac{3+\sqrt{21}}{2}$��$\frac{31}{8}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1������ƽ������1 | B�� | -0.1��0.01��ƽ���� | ||
| C�� | $\sqrt{81}$=��9 | D�� | $\frac{9}{16}$��ƽ������$\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com