
在平面直角坐标系xOy中,设点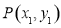 ,
,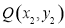 是图形W上的任意两点.
是图形W上的任意两点.
定义图形W的测度面积:若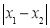 的最大值为m,
的最大值为m,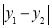 的最大值为n,则
的最大值为n,则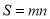 为图形W的测度面积.
为图形W的测度面积.
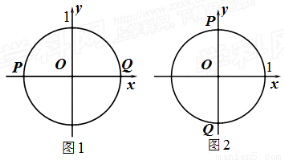
例如,若图形W是半径为1的⊙O.当P,Q分别是⊙O与x轴的交点时,如图1,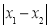 取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,
取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,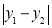 取得最大值,且最大值n=2.则图形W的测度面积
取得最大值,且最大值n=2.则图形W的测度面积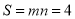 .
.
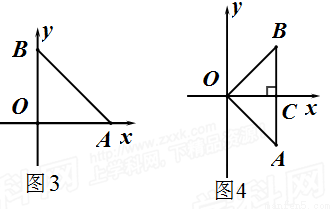
(1)若图形W是等腰直角三角形ABO,OA=OB=1.
①如图3,当点A,B在坐标轴上时,它的测度面积S= ;
②如图4,当AB⊥x轴时,它的测度面积S= ;
(2)若图形W是一个边长为1的正方形ABCD,则此图形测度面积S的最大值为 ;
(3)若图形W是一个边长分别为3和4的矩形ABCD,求它的测度面积S的取值范围.
(1)①1;②1;(2)2;(3) .
.
【解析】
试题分析:(1)①根据给出的定义可以求出来;
②根据给出的定义可以求出来;
(2)根据定义可以求出测度面积的最大值为2;
(3)因为平移图形W不会改变其测度面积S的大小,将矩形ABCD的其中一个顶点B平移至x轴上,注意分三种情况讨论,
试题解析:(1)① 1;
② 1.
(2) 2.
(3)不妨设矩形ABCD的边AB=4,BC=3.由已知可得,平移图形W不会改变其测度面积S的大小,将矩形ABCD的其中一个顶点B平移至x轴上.
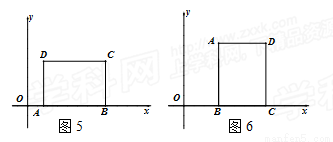
当顶点A,B或B,C都在x轴上时,如图5和图6,矩形ABCD的测度面积S就是矩形ABCD的面积,此时S取得最小值,且最小值为12.
当顶点A,C都不在x轴上时,如图7.
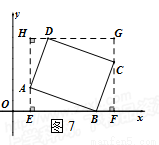
过A作直线AE⊥x轴于点E,过C作直线CF⊥x轴于点F,过D作直线GH∥x轴,与直线AE,CF分别交于点H和点G,则可得四边形EFGH是矩形.
当点P,Q分别与点A,C重合时,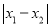 取得最大值
取得最大值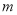 ,且最大值
,且最大值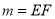 ;
;
当点P,Q分别与点B,D重合时,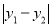 取得最大值
取得最大值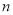 ,且最大值
,且最大值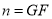 .
.
∴图形W的测度面积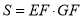 .
.
∵∠ABC=90°,∴∠ABE+∠CBF=90°,∵∠AEB=90°,∴∠ABE+∠BAE=90°,∴∠BAE=∠CBF.
又∵ ,∴△ABE∽△BCF,∴
,∴△ABE∽△BCF,∴ .
.
设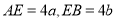
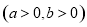 ,则
,则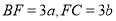 ,
,
在Rt△ABE中,由勾股定理得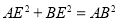 .
.
∴ .即
.即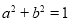 .∵
.∵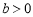 ,∴
,∴ ,易证△ABE≌△CDG.∴
,易证△ABE≌△CDG.∴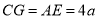 .∴
.∴ ,
,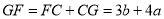 .
.
∴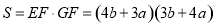
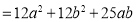
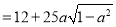
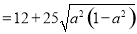
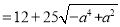

∴当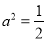 ,即
,即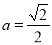 时,测度面积S取得最大值
时,测度面积S取得最大值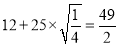 .
.
∵ ,∴
,∴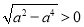 .∴
.∴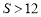 .
.
∴当顶点A,C都不在x轴上时,S的范围为 .
.
综上所述,测度面积S的取值范围是 .
.
考点:1.新定义;2.勾股定理.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源:2014-2015学年北京市通州区九年级上学期期末考试数学试卷(解析版) 题型:解答题
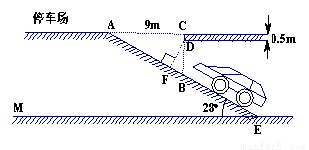
某大型超市为了缓解停车难的问题,建筑设计师提供了楼顶停车场的设计示意图(如图AC与ME平行).按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.请根据下图求出汽车通过坡道口的限高DF的长.(结果精确到0.1m)
(参考数据: sin28°≈0.47,cos28°≈0.88, tan28°≈0.53)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市石景山区九年级上学期期末考试数学试卷(解析版) 题型:填空题
二次函数 的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形An﹣1BnAnCn的周长为 .
的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形An﹣1BnAnCn的周长为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市海淀区九年级上学期期末考试数学试卷(解析版) 题型:解答题
某工厂生产的某种产品按质量分为10个档次,据调研显示,每个档次的日产量及相应的单件利润如下表所示(其中x为正整数,且1≤x≤10):

为了便于调控,此工厂每天只生产一个档次的产品.当生产质量档次为x的产品时,当天的利润为y万元.
(1)求y关于x的函数关系式;
(2)工厂为获得最大利润,应选择生产哪个档次的产品?并求出当天利润的最大值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市丰台区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,PB切 于点B,联结PO并延长交
于点B,联结PO并延长交 于点E,过点B作BA⊥PE交
于点E,过点B作BA⊥PE交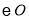 于点A,联结AP,AE.
于点A,联结AP,AE.

(1)求证:PA是 的切线;
的切线;
(2)如果OD=3,tan∠AEP=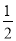 ,求
,求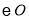 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市东城区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
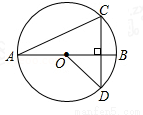
A.120° B.140° C.150° D.160°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com