
【题目】已知四边形ABCD是正方形,点P,Q在直线BC上,且AP∥DQ,过点Q作QO⊥BD,垂足为点O,连接OA,OP.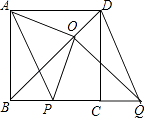
(1)如图,点P在线段BC上,
①求证:四边形APQD是平行四边形;
②判断OA,OP之间的数量关系和位置关系,并加以证明;
(2)若正方形ABCD的边长为2,直接写出BP=1时,△OBP的面积.
【答案】
(1)①证明:∵四边形ABCD是正方形,
∴AD∥BC,
∵AP∥DQ,
∴四边形APQD为平行四边形;
②解:结论:OA=OP,OA⊥OP,理由如下:
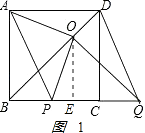
∵四边形ABCD是正方形,
∴AB=BC=PQ,∠ABO=∠OBQ=45°,
∵OQ⊥BD,
∴∠PQO=45°,
∴∠ABO=∠OBQ=∠PQO=45°,
∴OB=OQ,
在△AOB和△OPQ中,
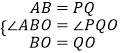 ,
,
∴△AOB≌△POQ(SAS),
∴OA=OP,∠AOB=∠POQ,
∴∠AOP=∠BOQ=90°,
∴OA⊥OP
(2)解:如图,过O作OE⊥BC于E.
①如图1,当P点在B点右侧时,
则BQ=1+2=3,OE= ![]() BQ=
BQ= ![]() ,
,
∴S△OPB= ![]() ×1×
×1× ![]() =
= ![]()
②如图2,当P点在B点左侧时,
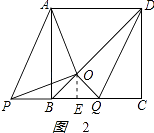
则BQ=2﹣1=1,OE= ![]() BQ=
BQ= ![]() ,
,
∴S△PBO= ![]() ×1×
×1× ![]() =
= ![]() ,
,
综上所述,△POB的面积为 ![]() 或
或 ![]() .
.
【解析】①由四边形ABCD是正方形,得到AD∥BC,已知AP∥DQ,得到四边形APQD为平行四边形;由正方形的性质得AB=BC=PQ,∠ABO=∠OBQ=45°,已知OQ⊥BD,得到∠ABO=∠OBQ=∠PQO=45°,得到OB=OQ,得到△AOB≌△POQ(SAS),得到OA=OP,∠AOB=∠POQ=90°,即OA⊥OP;②当P点在B点右侧时,则BQ=1+2=3,OE= BQ![]() 2= 3
2= 3![]() 2 ,求出△OPB的面积;当P点在B点左侧时,则BQ=2﹣1=1,OE=BQ
2 ,求出△OPB的面积;当P点在B点左侧时,则BQ=2﹣1=1,OE=BQ![]() 2= 1
2= 1![]() 2,求出△OPB的面积.
2,求出△OPB的面积.
【考点精析】本题主要考查了平行四边形的判定与性质和正方形的性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,坐标平面上,△ABC≌△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC,若A、B、C的坐标分别为(﹣3,1)、(﹣6,﹣3)、(﹣1,﹣3),D、E两点在y轴上,则F点到y轴的距离为 . 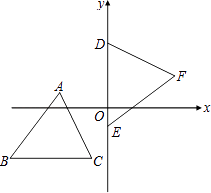
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地球的表面积约为510000000km2 , 将510000000用科学记数法表示为( )
A.0.51×109
B.5.1×109
C.5.1×108
D.0.51×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=∠C,点E,F分别在边AB,BC上,AE=DF=DC.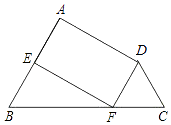
(1)若∠DFC=70°,则∠C的大小=(度),∠B的大小=(度);
(2)求证:四边形AEFD是平行四边形;
(3)若∠FDC=2∠EFB,则四边形AEFD一定是“菱形、矩形、正方形”中的 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将![]() 纸片沿中位线
纸片沿中位线![]() 折叠,使点
折叠,使点![]() 的对称点
的对称点![]() 落在
落在![]() 边上,再将纸片分别沿等腰
边上,再将纸片分别沿等腰![]() 和等腰
和等腰![]() 的底边上的高线
的底边上的高线![]() ,
,![]() 折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
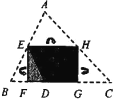
(1)将![]() 纸片按图2的方式折叠成一个叠合矩形
纸片按图2的方式折叠成一个叠合矩形![]() ,则操作形成的折痕分别是线段_____,_____;
,则操作形成的折痕分别是线段_____,_____;![]() ______.
______.
(2)![]() 纸片还可以按图3的方式折叠成一个叠合矩形
纸片还可以按图3的方式折叠成一个叠合矩形![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
(3)如图4,四边形![]() 纸片满足
纸片满足![]() .小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出
.小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出![]() 的长.
的长.
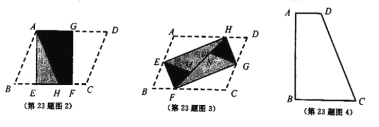
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快餐店共有10名员工,所有员工工资的情况如下表:
人员 | 店长 | 厨师甲 | 厨师乙 | 会计 | 服务员甲 | 服务员乙 | 勤杂工 |
人数 | 1 | 1 | 1 | 1 | 1 | 3 | 2 |
工资额 | 20000 | 7000 | 4000 | 2500 | 2200 | 1800 | 1200 |
请解答下列问题:
(1)餐厅所有员工的平均工资是;所有员工工资的中位数是 .
(2)用平均数还是用中位数描述该餐厅员工工资的一般水平比较恰当?
(3)去掉店长和厨师甲的工资后,其他员工的平均工资是多少?它是否也能反映该快餐店员工工资的一般水平?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com