
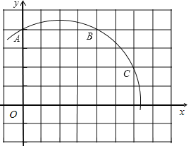
【题目】如图,在平面直角坐标系中,![]() ,则经过
,则经过![]() 三点的圆弧所在圆的圆心
三点的圆弧所在圆的圆心![]() 的坐标为__________;点
的坐标为__________;点![]() 坐标为
坐标为![]() ,连接
,连接![]() ,直线
,直线![]() 与
与![]() 的位置关系是___________.
的位置关系是___________.
【答案】(2,0) 相切
【解析】
由网格容易得出AB的垂直平分线和BC的垂直平分线,它们的交点即为点M,根据图形即可得出点M的坐标;由于C在⊙M上,如果CD与⊙M相切,那么C点必为切点;因此可连接MC,证MC是否与CD垂直即可.可根据C、M、D三点坐标,分别表示出△CMD三边的长,然后用勾股定理来判断∠MCD是否为直角.
解:如图,作线段AB,CD的垂直平分线交点即为M,由图可知经过A、B、C三点的圆弧所在圆的圆心M的坐标为(2,0).
连接MC,MD,
∵MC2=42+22=20,CD2=42+22=20,MD2=62+22=40,
∴MD2=MC2+CD2,∴∠MCD=90°,
又∵MC为半径,
∴直线CD是⊙M的切线.

故答案为:(2,0);相切.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】11月21日,“中国流动科技馆”榆林市第二轮巡展启动仪式在榆阳区青少年校外活动中心盛大举行,此次巡展以“体验科学”为主题.榆林市某中学举行了“科普知识”竞赛,为了解此次“科普知识”竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如下的不完整的统计表和统计图,如图所示.请根据图表信息解答以下问题.
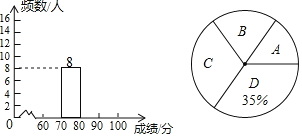

(1)表中a= ;一共抽取了 个参赛学生的成绩;
(2)补全频数分布直方图;
(3)计算扇形统计图中“B”与“C”对应的圆心角度数;
(4)若成绩在80分以上(包括80分)的为“优”等,所抽取学生成绩为“优”的占所抽取学生的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线![]() 的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
①2b﹣c=2;②a=![]() ;③ac=b﹣1;④
;③ac=b﹣1;④![]() >0
>0
其中正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
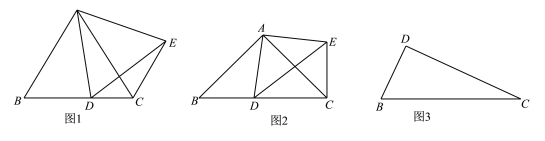
【题目】如图1,在△ABC中,AB=AC,∠BAC=60°,D为BC边上一点,(不与点B、C)重合,将线段AD绕点A逆时针旋转60°得到AE,连接EC,则∠ACE的度数是__________,线段AC,CD,CE之间的数量关系是_______________.
(2)2,在△ABC中,AB=AC,∠BAC=90°,D为BC边上一点(不与点B、C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,请写出∠ACE的度数及线段AD,BD,CD之间的数量关系,并说明理由.
(3)如图3,在Rt△DBC中,DB=3,DC=5,∠BDC=90°,若点A满足AB=AC,∠BAC=90°,请直接写出线段AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是OB,OD的中点.
(1)试说明四边形AECF是平行四边形.
(2)若AC=8,AB=6.若AC⊥AB,求线段BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某林业部门要考察某幼苗的成活率,于是进行了试验,下表中记录了这种幼苗在一定条件下移植的成活情况,则下列说法不正确的是( )
移植总数 | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
成活数 | 369 | 1335 | 3203 | 6335 | 8073 | 12628 |
成活的频率 | 0923 | 0.890 | 0915 | 0.905 | 0.897 | 0.902 |
A.由此估计这种幼苗在此条件下成活的概率约为0.9
B.如果在此条件下再移植这种幼苗20000株,则必定成活18000株
C.可以用试验次数累计最多时的频率作为概率的估计值
D.在大量重复试验中,随着试验次数的增加,幼苗成活的频率会越来越稳定,因此可以用频率估计概率
查看答案和解析>>
科目:初中数学 来源: 题型:
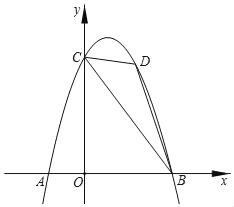
【题目】如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C,点D是抛物线上一个动点,设点D的横坐标为m(1<m<4)连接BC,DB,DC.
(1)求抛物线的函数解析式;
(2)△BCD的面积是否存在最大值,若存在,求此时点D的坐标;若不存在,说明理由;
(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
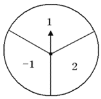
【题目】如图,一转盘被等分成三个扇形,上面分别标有-1,1,2中的一个数,指针固定,转动转盘后任其自由停止,这时某个扇形会恰好停在指针所指的位置,并相应得到这个扇形上的数( 若指针恰好指在等分线上,当做指向右边的扇形).若转动一次转盘,将所得的数作为k,则使反比例函数![]() 的图象在第一、三象限的概率是多少?若小静和小宇进行游戏,每人各转动两次转盘,若两次所得数的积为正数,则小静赢,若两次所得数的积为负数,则小宇赢.这是个公平的游戏吗?请说明理由.(借助画树状图或列表的方法)
的图象在第一、三象限的概率是多少?若小静和小宇进行游戏,每人各转动两次转盘,若两次所得数的积为正数,则小静赢,若两次所得数的积为负数,则小宇赢.这是个公平的游戏吗?请说明理由.(借助画树状图或列表的方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)用配方法解方程:x2﹣4x+2=0;
(2)如图,在平面直角坐标系中,△ABC的顶点均在格点上,将△ABC绕原点O逆时针方向旋转90°得到△A1B1C1.请作出△A1B1C1,写出各顶点的坐标,并计算△A1B1C1的面积.
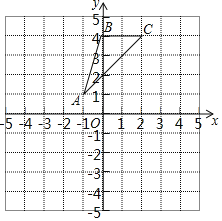
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com