
����Ŀ����֪��������![]() ��������ԭ�㣬�ҵ�
��������ԭ�㣬�ҵ�![]() ʱ, y��x���������С.
ʱ, y��x���������С.
��1���������ߵĽ���ʽ��
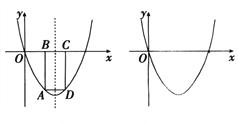
��2������ͼ�����A�Ǹ���������λ��x���·���һ�����㣬����A��x���ƽ���߽�����������һ��D������AB![]() x���ڵ�B, DC
x���ڵ�B, DC![]() x���ڵ�C.
x���ڵ�C.
�ٵ� BC=1ʱ��ֱ��д������ABCD���ܳ���
���趯��A������Ϊ��a, b��,������ABCD���ܳ�L��ʾΪa�ĺ�������д���Ա�����ȡֵ��Χ���ж��ܳ��Ƿ�������ֵ��������ڣ����������ֵ���������ʱ��A�����ꣻ��������ڣ���˵������.
���𰸡���1��![]() ����2����6 ����L=
����2����6 ����L= ����A��������
����A��������![]() ����
����![]() ����
����![]() ����
����![]() ����L�����ֵΪ
����L�����ֵΪ![]() ��
��
�������������������1��������֪�������߹���0��0�������Խ���0��0������y=x2+��2m��1��x+m2��1�������m��ֵ������x��0ʱ��y��x���������С����֪�Գ���һ����y����Ҳ࣬�����ó�m��ȡֵ��Χ��
��2������AD��x�ᣬ����A��D���������ߵĶԳ���Գƣ��Ӷ��ó�B�ĺ����꣬���������߽���ʽ�������B�������꣬�Ӷ��ó�AB�ij��ȣ�
����A��a��b������y=x2��3x������b=a2��3a�����öԳ��Կ����D������Ϊ��3��a��a2��3a��������AD=|3��2a|��Ȼ�����������������ۣ�0��a��![]() ʱ��
ʱ��![]() ��a��3ʱ���ֱ����L��a�Ĺ�ϵʽ�����ö��κ��������ʼ������L����ֵ��
��a��3ʱ���ֱ����L��a�Ĺ�ϵʽ�����ö��κ��������ʼ������L����ֵ��
����������⣺��1���ѣ�0��0������y=x2+��2m��1��x+m2��1����0=m2��1����m=��1������x��0ʱ��y��x���������С�����Գ���x=![]() ��0����m��
��0����m��![]() ����m=��1���������ߵĽ���ʽΪy=x2��3x��
����m=��1���������ߵĽ���ʽΪy=x2��3x��
��2���١�AD��x�ᣬ��A��D���������ߵĶԳ���Գƣ��������ߵĶԳ���Ϊx=![]() ��BC=1
��BC=1
����B�ĺ�����Ϊ1������x=1����y=x2��3x����y=��2����AB=2��������ABCD���ܳ�Ϊ��2��2+2��1=6��
����A��a��b������y=x2��3x����b=a2��3a����A��a��a2��3a������y=0����y=x2��3x����x=0��x=3����������֪��0��a��3����AB=3a��a2��������֪��A��D����x=![]() �Գƣ���D������Ϊ��3��a��a2��3a������AD=|3��a��a|=|3��2a|��������������ۣ�
�Գƣ���D������Ϊ��3��a��a2��3a������AD=|3��a��a|=|3��2a|��������������ۣ�
��0��a��![]() ʱ����AD=3��2a����L=2��AB+AD��=��2a2+2a+6=��2��a��
ʱ����AD=3��2a����L=2��AB+AD��=��2a2+2a+6=��2��a��![]() ��2+
��2+![]() ����a=
����a=![]() ʱ��L�����ֵΪ
ʱ��L�����ֵΪ![]() ����ʱA������Ϊ��
����ʱA������Ϊ��![]() ����
����![]() ����
����
��![]() ��a��3ʱ����AD=2a��3����L=2��AB+AD��=
��a��3ʱ����AD=2a��3����L=2��AB+AD��=![]() =��2��a��
=��2��a��![]() ��2+
��2+![]() ����a=
����a=![]() ʱ��L�����ֵΪ
ʱ��L�����ֵΪ![]() ����ʱA������Ϊ��
����ʱA������Ϊ��![]() ����
����![]() ����
����
����������L=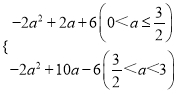 ����A��������
����A��������![]() ����
����![]() ����
����![]() ����
����![]() ����L�����ֵΪ
����L�����ֵΪ![]() ��
��


 ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ��4����ȫ��ͬ��С�ֱ��������1��2��3��4��������һ������������ת��Բ�̣����ֳ������ȵ�3���������ֱ��������1��2��3����ͼ��ʾ����

��1���ӿڴ�������һ��С���������ϵ����ִ���2�ĸ���Ϊ ��
��2��С����С����ͨ����Ϸ������˭����ѧУ�μӸ�ӽ��������Ϸ����Ϊ��һ�˴ӿڴ�������һ��С����һ��ת��Բ�̣�����������ϵ�������Բ����ת������֮��С��5����ôС��ȥ������С��ȥ������Ϊ��Ϸ��ƽ��������״ͼ���б���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�F��CD��һ�㣬E��BF��һ�㣬����AE��AC��DE����AB=AC��AD=AE����BAC=��DAE=70����AEƽ�֡�BAC�������н����У�����ABE�ա�ACD����BE=EF���ۡ�BFD=110������AC��ֱƽ��DE����ȷ�ĸ����У�������

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������������棬����һ�������˱��Σ�����һ����������ǣ� ����
A. �������� B. ���ı��� C. ������� D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ������A��B���ֽ�Ʒ�������ɼ������ͬѧ����֪����1��A��Ʒ��1��B��Ʒ����18Ԫ������30��A��Ʒ��20��B��Ʒ����480Ԫ.
��1��A��B���ֽ�Ʒ�ĵ��۷ֱ��Ƕ���Ԫ��
��2�����ѧУ�������ֽ�Ʒ��100�����ܷ��ò�����850Ԫ����ô�����Թ���A��Ʒ���ټ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳����ͼ1��AB��CD�� ![]() ,
,![]() ����
����![]() ������
������

С����˼·�ǣ���ͼ2����P��PE��AB��ͨ��ƽ�������ʣ��ɵ�![]() _______��
_______��
����Ǩ�ƣ���ͼ3��AD��BC����P������OM���˶��� ![]() ��
�� ![]() ��
��
��1������P��A��B����֮���˶�ʱ�� ![]() ��
��![]() ��
��![]() ֮���к�������ϵ����˵������.
֮���к�������ϵ����˵������.
��2�������P��A��B��������˶�ʱ����P���A��B��O���㲻�غϣ�������ֱ��д��![]() ��
��![]() ��
��![]() ֮���������ϵ��
֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��Ƹ�˲ţ���ӦƸ�߷ֱ�����Ķ�������רҵ֪ʶ����������������ԣ�����������Ե÷ְ�3��5��2�ı���ȷ��ÿ�˵����ճɼ��������Ӽ�����ѡ����¼ȡһ�ˣ���֪���˵ĸ�����Ե÷����±�(��λ����)
�Ķ� | רҵ | ���� | |
�� | 93 | 86 | 73 |
�� | 95 | 81 | 79 |
����ͨ����صļ���˵��˭����¼�ã�
�������ѡ�߽���ӦƸ��Щ�����Ľ��飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ȫ�ȵ�ֱ�������Ρ�ABD����ACEƴ��һ��ͼ��1���������ABD������
��1��������ACE�Ƶ�A��ʱ����ת������DE��M��DE���е㣬����MB��MC��ͼ��2������֤����MB=MC��
��2������ͼ��1���е�CE����ƽ�ƣ���CAE���䣬����DE��M��DE���е㣬����MB��MC��ͼ��3�������ж�MB��MC��������ϵ����˵�����ɣ�
��3���ڣ�2���У�����CAE�Ĵ�С�ı䣨ͼ��4�����������������䣬��2���е�MB��MC��������ϵ��������˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ���������ܱ�ʾ����������ż����ƽ�����ô���������Ϊ����������.
�磺![]()
![]()
![]()
��ˣ�4��12��20������������������.
��1��28��2012���������Dz�����������Ϊʲô��
��2������������ż��Ϊ![]() ��
��![]() (����
(����![]() Ϊ�Ǹ�����)��������������ż���������������4�ı�������˵������.
Ϊ�Ǹ�����)��������������ż���������������4�ı�������˵������.
��3����������������ƽ���ȡ�������Dz�������������˵������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com