
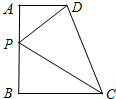
 如图所示,在直角梯形ABCD中,AB=7,AD=2,BC=3,如果AB上的点P,△PAD与△PBC相似,那么这样的点有( )
如图所示,在直角梯形ABCD中,AB=7,AD=2,BC=3,如果AB上的点P,△PAD与△PBC相似,那么这样的点有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据相似三角形的性质分情况讨论得出AP的长,即可得到满足题意的点P的个数.
解答 解:分两种情况:
①如果△PAD∽△PBC,
则PA:PB=AD:BC=2:3,
又PA+PB=AB=7,
∴AP=7×2÷5=2.8;
②如果△PAD∽△CBP,
则PA:BC=AD:BP,
即PA•PB=2×3=6,
又∵PA+PB=AB=7,
∴PA、PB是一元二次方程x2-7x+6=0的两根,
解得x1=1,x2=6,
∴AP=1或6.
综上,可知AP=2.8或1或6.
∴满足题意的点P的个数为3个,
故选C.
点评 本题主要考查了相似三角形的判定及性质,难度适中,进行分类讨论以及熟练掌握相似三角形的各种判定方法是解题的关键.


科目:初中数学 来源: 题型:解答题
 某校为了解七年级学生课外学习情况,随机抽取了部分学生作调查,通过调查将获得的数据按性别绘制成如下的女生频数分布表和如图所示的男生频数分布直方图:
某校为了解七年级学生课外学习情况,随机抽取了部分学生作调查,通过调查将获得的数据按性别绘制成如下的女生频数分布表和如图所示的男生频数分布直方图:| 学习时间t(分钟) | 人数 | 占女生人数百分比 |
| 0≤t<30 | 4 | 20% |
| 30≤t<60 | m | 15% |
| 60≤t<90 | 5 | 25% |
| 90≤t<120 | 6 | n |
| 120≤t<150 | 2 | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com