
【题目】直线y=﹣x+2与x轴、y轴分别交于点A、点C,抛物线经过点A、点C,且与x轴的另一个交点为B(﹣1,0).
(1)求抛物线的解析式;
(2)点D为第一象限内抛物线上的一动点.
①如图1,若CD=AD,求点D的坐标;
②如图2,BD与AC交于点E,求S△CDE:S△CBE的最大值.

【答案】(1)y=﹣x2+x+2;(2)①D(![]() ,
,![]() );②S△CDE:S△CBE的最大值为
);②S△CDE:S△CBE的最大值为![]() .
.
【解析】分析:(1)先求出A、C的坐标,再利用待定系数法求出函数的解析式;
(2)①根据等腰直角三角形的性质,确定点D的在y=x上,设出点D的坐标,代入y=﹣x2+x+2即可得到函数的解析式;
②作DF∥y轴交AC于F,BG∥y轴交直线AC于G,证得△DEF∽△BEG,然后根据相似三角形的面积比与相似比的关系,设出D点的坐标(t,﹣t2+t+2),再根据相似比的性质和二次函数的最值求解即可.
详解:(1)当x=0时,y=﹣x+2=2,则C(0,2),
当y=0时,﹣x+2=0,解得x=2,则A(2,0),
设抛物线解析式为y=a(x+1)(x﹣2),
把C(0,2)代入得a1(﹣2)=2,解得a=﹣1,
∴抛物线解析式为y=﹣(x+1)(x﹣2),
即y=﹣x2+x+2;
(2)①∵OA=OC,
∴△OAC为等腰直角三角形,
∵DC=DA,
∴点D在AC的垂直平分线上,
即点D在直线y=x上,
设D(m,m)(m>0),
把D(m,m)代入y=﹣x2+x+2得﹣m2+m+2=m,解得m1=![]() ,m2=﹣
,m2=﹣![]() (舍去),
(舍去),
∴点D的坐标为(![]() ,
,![]() );
);
②作DF∥y轴交AC于F,BG∥y轴交直线AC于G,如图2,
∵DF∥BG,
∴△DEF∽△BEG,
∴![]() =
=![]() ,
,
∵S△CDE:S△CBE=![]() ,
,
∴S△CDE:S△CBE=![]() ,
,
当x=﹣1时,y=﹣x+2=3,则G(﹣1,3),
设D(t,﹣t2+t+2)(0<t<2),则F(t,﹣t+2),
∴DF=﹣t2+t+2﹣(﹣t+2)=﹣t2+2t,
∴S△CDE:S△CBE=![]() =
=![]() =﹣
=﹣![]() (t﹣1)2+
(t﹣1)2+![]() ,
,
∴当t=1时,S△CDE:S△CBE的最大值为![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
【题目】如下图,将边长为 9cm 的正方形纸片 ABCD 折叠,使得点 A 落在边 CD 上的 E 点,折痕为 MN.若 CE 的长为 6cm,则 MN 的长为_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O 为直线 AB 上一点,过点 O 作射线 OC,使∠BOC=135°,将一个含 45°角的直角三角尺的一个顶点放在点 O 处,斜边 OM 与直线 AB 重合,另外两条直角边都在直线 AB 的下方.
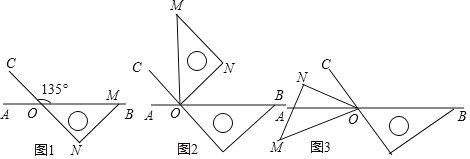
(1)将图 1 中的三角尺绕着点 O 逆时针旋转 90°,如图 2 所示,此时∠BOM= 度(答案直接填写在答题卡的横线上);在图 2 中,OM 是否平分∠CON ? 请说明理由;
(2)紧接着将图 2 中的三角板绕点 O 逆时针继续旋转到图 3 的位置所示,使得 ON 在∠AOC 的内部,请探究:∠AOM 与∠CON 之间的数量关系,并说明理由;
(3)将图 1 中的三角板绕点 O 按每秒 5°的速度沿逆时针方向旋转一周,在旋转的过程中, 第 t 秒时,直线 ON 恰好平分锐角∠AOC,请你直接写出t 的值为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC,∠C=90°.
(1)求作:△ABC的内切圆⊙O;(尺规作图,不写作法,保留痕迹)
(2)在(1)中,∠AOB的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
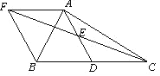
【题目】如图,在![]() 中,D是BC的中点,E是AD的中点,过点A作
中,D是BC的中点,E是AD的中点,过点A作![]() ,AF与CE的延长线相交于点F,连接BF.
,AF与CE的延长线相交于点F,连接BF.
(1)求证:四边形AFBD是平行四边形;
(2)①若四边形AFBD是矩形,则![]() 必须满足条件_________;
必须满足条件_________;
②若四边形AFBD是菱形,则![]() 必须满足条件_________.
必须满足条件_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MAN=30°,点O为边AN上一点,以O为圆心,4为半径
作⊙O交AN于D、E两点.
⑴ 当⊙O与AM相切时,求AD的长;
⑵ 如果AD=2,那么AM与⊙O又会有怎样的位置关系?并说明理由.
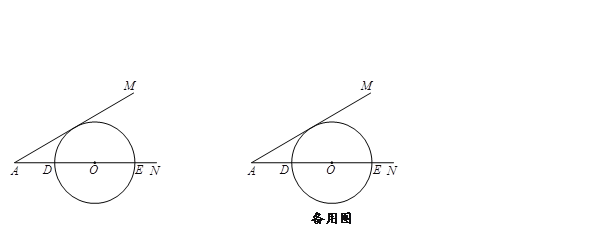
查看答案和解析>>
科目:初中数学 来源: 题型:
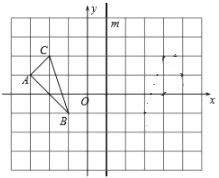
【题目】如图,在平面直角坐标系中,![]() 的顶点坐标分别为
的顶点坐标分别为![]() 、
、![]() 、
、![]() .
.
(1)不用画图,请直接写出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() 的三个顶点的坐标:
的三个顶点的坐标:![]() ,
,![]() ,
,![]() ;
;
(2)在图中画出![]() 关于直线
关于直线![]() (直线
(直线![]() 上各点的横坐标都为1)对称的图形
上各点的横坐标都为1)对称的图形![]() ,并直接写出三个顶点的坐标:
,并直接写出三个顶点的坐标:![]() ,
,![]() ,
,![]() ;
;
(3)若![]() 内有任意一点
内有任意一点![]() 的坐标为
的坐标为![]() ,则在
,则在![]() 关于直线
关于直线![]() (直线
(直线![]() 上各点的横坐标都为1)对称的图形
上各点的横坐标都为1)对称的图形![]() 上,点
上,点![]() 的对应点
的对应点![]() 的坐标 .(用含
的坐标 .(用含![]() 和
和![]() 的式子表示)
的式子表示)
(建议:先用铅笔画图,确定无误后用黑色水性笔画在答题卡上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com