练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．已知$\frac{1}{1+a}$+$\frac{1}{1+b}$=$\frac{2}{1+ab}$，α+b≠0，求证ab=1．

    分析 将等式进行化简即可求出ab=1

    解答 解：∵$\frac{1}{1+a}$+$\frac{1}{1+b}$=$\frac{2}{1+ab}$，a+b≠0
    ∴左边=$\frac{1+b+1+a}{（1+a）（1+b）}$=$\frac{2+a+b}{（1+a）（1+b）}$=$\frac{2}{1+ab}$=右边
    ∴（2+a+b）（1+ab）=2（1+a）（1+b）
    ∴2+2ab+a+a2b+b+ab2=2（1+b+a+ab）=2+2b+2a+2ab
    ∴a2b+ab2=a+b
    ∴ab（a+b）=a+b
    ∴ab=1

    点评 本题考查等式的证明，涉及分式运算以及整式运算的法则，属于中等题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．（1）计算：（8a-7b）-（4a-5b）
    （2）解方程：$\frac{x+1}{2}$=3$+\frac{2-x}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，△ABC中，∠B=45°，AB=3$\sqrt{2}$，D是BC中点，tanC=$\frac{1}{5}$．
    求：
    （1）BC的长； 
    （2）sin∠ADB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．解下列分式方程：
    （1）$\frac{x}{x-2}$-1=$\frac{8}{{x}^{2}-4}$
    （2）$\frac{2}{x-1}$=$\frac{x+3}{{x}^{2}-1}$$+\frac{3}{x+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．在如图的网格图中，每个小正方形的边长均为1个单位，在Rt△ABC中，∠C=90°，AC=3，BC=4．
    （1）试在图中做出△ABC以A为旋转中心，沿顺时针方向旋转90°后的图形△AB1C1；
    （2）若点B的坐标为（-3，5），试在图中画出平面直角坐标系，并标出A、C两点的坐标；
    （3）根据（2）的坐标系，以B为位似中心，做△BA2C2，使△BA2C2与△ABC位似，且△BA2C2与△ABC位似比为2：1，并直接写出A2的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

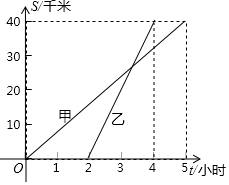    9．甲、乙两人沿相同的路线由A地到B地匀速前进，已知A，B两地间的距离为40千米，它们前进的路程记为s（单位：千米），甲出发后的时间记为t（单位：小时），甲、乙前进的路程与时间的函数图象如图所示，根据图象信息回答下列问题：
    （1）甲的速度是8千米/小时，乙比甲晚出发2小时；
    （2）分别求出甲、乙两人前进的路程S甲、S乙与甲出发后的时间t之间的函数关系式；
    （3）乙经过多长时间可以追上甲，此时两人距离B地还有多远？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．一只不透明的袋子中装有1个白球和2个红球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，记录颜色后放回，搅匀，再从中任意摸出1个球．
    （1）请用画树状图或列表的方法列出所有可能出现的结果；
    （2）求两次摸到“一只白球、一只红球”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知反比例函数y=$\frac{k}{x}$的图象经过点P（-1，-1）．
    （1）求此函数的表达式；
    （2）画出此函数在第一象限内的图象．
    （3）根据函数图象写出此函数的一条性质．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，点C在线段AB上，AC=6cm，MB=10cm，点M，N分别为AC，BC的中点．
    （1）求线段BC，MN的长；
    （2）若C在线段AB的延长线上，且满足AC-BC=acm，M，N分别是线段AC，BC的中点，请画出图形，并用a的式子表示MN的长度．

    查看答案和解析>>

    同步练习册答案