
ЁОЬтФПЁПдкСтаЮABCDжаЃЌЕуQЮЊABБпЩЯвЛЕуЃЌЕуFЮЊBCБпЩЯвЛЕуСЌНгDQЁЂDFКЭQFЃЎ
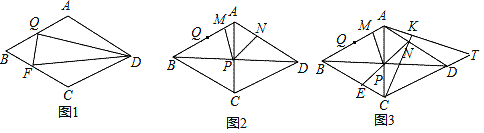
ЃЈ1ЃЉШчЭМ1ЃЌШєЁЯADQ=ЁЯFDQЃЌЁЯFQD=90ЁуЃЌЧѓжЄЃКAQ=BQЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЁЯBAD=120ЁуЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуPЃЌвдЕуPЮЊЖЅЕузїЁЯMPN=60ЁуЃЌPMгыABНЛгкЕуMЃЌPNгыADНЛгкЕуNЃЌЧѓжЄЃКDN+QM=ABЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдкЃЈ1ЃЉЃЈ2ЃЉЕФЬѕМўЯТЃЌбгГЄNPНЛBCгкЕуEЃЌбгГЄCNЕНЕуKЃЌЪЙCK=CAЃЌСЌНгAKВЂбгГЄКЭCDЕФбгГЄЯпНЛгкЕуTЃЌШєAMЃКDN=1ЃК5ЃЌSЫФБпаЮMBEP=12![]() ЃЌЧѓЯпЖЮDTЕФГЄЃЎ
ЃЌЧѓЯпЖЮDTЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉDT=4ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉзїИЈжњЯпЃЌжЄУїЁїFQDЁеЁїLQDКЭЁїALQЁеЁїBFQЃЌПЩЕУНсТлЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгQPЃЌгЩAQ=BQЃЌВЂИљОнжБНЧШ§НЧаЮаББпжаЯпЕФаджЪЕУЃКPA=PQЃЌЫљвдЁїAPQЪЧЕШБпШ§НЧаЮЃЌжЄУїЁїPQMЁеЁїPANЃЈASAЃЉЃЌдђQM=ANЃЌИљОнAB=AD=DN+ANЃЌДњШыПЩЕУНсТлЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌзїИЈжњЯпЃЌЙЙНЈжБНЧЁїAMGКЭжБНЧЁїCEHЃЌЩшAM=aЃЌдђDN=5aЃЌИљОнЃЈ2ЃЉЃКAB=DN+QMЃЌЕУAB=8aЃЌжЄУїЁїPCEЁеЁїPANЃЌЕУCE=AN=3aЃЌИљОнЙДЙЩЖЈРэМЦЫуBPКЭMGЁЂEHЕФГЄЃЌИљОнSЫФБпаЮMBEP=12![]() ЃЌСаЗНГЬПЩЕУaЕФжЕЃЌ
ЃЌСаЗНГЬПЩЕУaЕФжЕЃЌ
дђAM=1ЃЌAN=3ЃЌDN=5ЃЌCD=8ЃЌЙ§CзїCIЁЭADгкIЃЌЕУID=![]() CD=
CD=![]() ЁС8ЃН4ЃЌИљОнЙДЙЩЖЈРэЕУCNЕФГЄЃЛ
ЁС8ЃН4ЃЌИљОнЙДЙЩЖЈРэЕУCNЕФГЄЃЛ
дкCDЩЯНиШЁCSЃЌЪЙCS=DN=5ЃЌСЌНгASЃЌжЄУїЁїACSЁеЁїCDNЃЈSASЃЉЃЌПЩЕУНсТлЃЎ
жЄУїЃКЃЈ1ЃЉШчЭМ1ЃЌЗжБ№бгГЄFQЁЂDAНЛгкLЃЌ
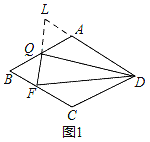
ЁпЁЯADQ=ЁЯFDQЃЌDQ=DQЃЌЁЯFQD=ЁЯLQD=90ЁуЃЌ
ЁрЁїFQDЁеЁїLQDЃЈASAЃЉЃЌ
ЁрFQ=LQЃЌ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрLDЁЮBFЃЌ
ЁрЁЯALQ=ЁЯBFQЃЌЁЯLAQ=ЁЯFBQЃЌ
ЁрЁїALQЁеЁїBFQЃЌ
ЁрAQ=BQЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгQPЃЌ
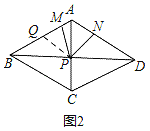
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрЁЯBAP=ЁЯDAPЃЌPA=PCЃЌACЁЭBDЃЌ
ЁрЁЯAPB=ЁЯAPD=90ЁуЃЌ
ЁпЁЯBAD=120ЁуЃЌ
ЁрЁЯBAP=ЁЯDAP=60ЁуЃЌ
ЁрЁЯABP=30ЁуЃЌ
ЁрPA=![]() ABЃЌ
ABЃЌ
ЁпAQ=BQЃЌ
ЁрPQ=![]() ABЃЌ
ABЃЌ
ЁрPA=PQЃЌ
ЁрЁїAPQЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯAPQ=ЁЯPQA=60ЁуЃЌ
ЁпЁЯMPN=60ЁуЃЌ
ЁрЁЯAPQ=ЁЯMPN=60ЁуЃЌ
ЁрЁЯQPM=ЁЯAPNЃЌ
ЁпЁЯPQM=ЁЯPAN=60ЁуЃЌ
ЁрЁїPQMЁеЁїPANЃЈASAЃЉЃЌ
ЁрQM=ANЃЌ
ЁпAB=AD=DN+ANЃЌ
ЁрAB=DN+QMЃЛ
ЃЈ3ЃЉНтЃКШчЭМ3ЃЌЙ§ЕуMзїMGЁЭACгкGЃЌЙ§ЕуEзїEHЁЭACгкHЃЌЩшAM=aЃЌ
ЁпAMЃКDN=1ЃК5ЃЌ
ЁрDN=5aЃЌ
гЩЃЈ2ЃЉжЊЃКAB=DN+QMЃЌ
ЁпAQ=![]() ABЃЌQM=AQЉAMЃЌ
ABЃЌQM=AQЉAMЃЌ
Ёр5a+![]() ABЉa=ABЃЌAB=8aЃЌ
ABЉa=ABЃЌAB=8aЃЌ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрADЁЮBCЃЌ
ЁрЁЯABC+ЁЯBAD=180ЁуЃЌ
ЁпЁЯBAD=120ЁуЃЌ
ЁрЁЯABC=60ЁуЃЌ
ЁрЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрAC=AB=8aЃЌ
ЁрAN=3aЃЌ
ЁпЁЯAPN=ЁЯCPEЃЌAP=CPЃЌЁЯDAC=ЁЯBCA=60ЁуЃЌ
ЁрЁїPCEЁеЁїPANЃЈASAЃЉЃЌ
ЁрCE=AN=3aЃЌ
RtЁїBPCжаЃЌЁЯCBP=30ЁуЃЌBC=8aЃЌ
ЁрBP=4![]() aЃЌ
aЃЌ
ЭЌРэMG=![]() aЃЌEH=
aЃЌEH=![]() aЃЌ
aЃЌ
ЁпSЫФБпаЮMBEP=SЁїABCЉSЁїAPMЉSЁїCPEЃЌ
Ёр![]() Љ
Љ![]() Љ
Љ![]() =12
=12![]() ЃЌ
ЃЌ
Ёрa2=1ЃЌa=1ЃЈa=Љ1ЩсШЅЃЉЃЌ
ЁрAM=1ЃЌAN=3ЃЌDN=5ЃЌCD=8ЃЌ
Й§CзїCIЁЭADгкIЃЌ
ЁрID=![]() =
=![]() ЃЌ
ЃЌ
ЁрNI=NDЉID=5Љ4=1ЃЌ
дкRtЁїCIDжаЃЌCD2=DI2+CI2ЃЌ
ЁрCI2=CD2ЉID2=82Љ42=48ЃЌ
дкRtЁїICNжаЃЌCN2=NI2+CI2ЃЌ
ЁрCN2=1+48=49ЃЌ
ЁрCN=7ЃЌ
дкCDЩЯНиШЁCSЃЌЪЙCS=DN=5ЃЌСЌНгASЃЌ
ЁрAN=SD=3ЃЌ
ЁпЁЯACS=ЁЯCDN=60ЁуЃЌAC=CDЃЌ
ЁрЁїACSЁеЁїCDNЃЈSASЃЉЃЌ
ЁрЁЯCAS=ЁЯDCNЃЌSA=NC=7ЃЌ
ЁпCA=CKЃЌ
ЁрЁЯCAK=ЁЯCKAЃЌ
ЁрЁЯSAK=ЁЯKTCЃЌ
ЁрSA=ST=7ЃЌ
ЁрDT=7Љ3=4ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОХФъМЖНЬЪІЖдЪдОэНВЦРПЮжабЇЩњВЮгыЕФЩюЖШгыЙуЖШНјааЦРМлЕїВщЃЌЦфЦРМлЯюФПЮЊжїЖЏжЪвЩЁЂЖРСЂЫМПМЁЂзЈзЂЬ§НВЁЂНВНтЬтФПЫФЯюЃЎЦРМлзщЫцЛњГщШЁСЫШєИЩУћГѕжабЇЩњЕФВЮгыЧщПіЃЌЛцжЦГЩШчЭМЫљЪОЕФЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЈОљВЛЭъећЃЉЃЌЧыИљОнЭМжаЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃК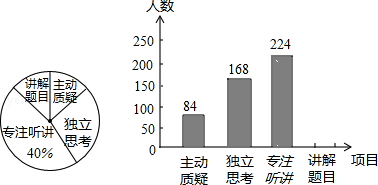
ЃЈ1ЃЉдкетДЮЦРМлжаЃЌвЛЙВГщВщСЫУћбЇЩњЃЛ
ЃЈ2ЃЉдкЩШаЮЭГМЦЭМжаЃЌЯюФПЁАжїЖЏжЪвЩЁБЫљдкЕФЩШаЮЕФдВаФНЧЕФЖШЪ§ЮЊЖШЃЛ
ЃЈ3ЃЉЧыНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ4ЃЉШчЙћШЋЪага6000УћОХФъМЖбЇЩњЃЌФЧУДдкЪдОэЦРНВПЮжаЃЌЁАЖРСЂЫМПМЁБЕФдМгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
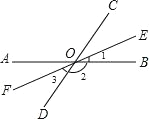
ЁОЬтФПЁПШчЭМЃЌжБЯп ABЁЂCD ЯрНЛгк OЃЌЁЯBOCЃН70ЁуЃЌOE ЪЧЁЯBOC ЕФНЧЦНЗжЯпЃЌOFЪЧOEЕФЗДЯђбгГЄЯпЃЎ
(1)ЧѓЁЯ1ЃЌЁЯ2ЃЌЁЯ3 ЕФЖШЪ§ЃЛ
(2)ХаЖЯ OF ЪЧЗёЦНЗжЁЯAODЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
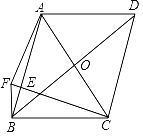
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЖдНЧЯпACКЭBDЯрНЛгкЕуOЃЌдкABЩЯгавЛЕуEЃЌСЌНгCEЃЌЙ§ЕуBзїBCЕФДЙЯпКЭCEЕФбгГЄЯпНЛгкЕуFЃЌСЌНгAFЃЌЁЯABF=ЁЯFCBЃЌFC=ABЃЌШєFB=1ЃЌAF=![]() ЃЌдђBD=_____ЃЎ
ЃЌдђBD=_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКдкЫФБпаЮABCDжаЃЌЁЯABC=ЁЯDCB=90ЁуЃЌЕуPдкBCБпЩЯЃЌСЌНгAPКЭPDЃЌЕуEдкDCБпЩЯЃЌСЌНгBEгыDPКЭAPЗжБ№НЛгкЕуFКЭЕуGЃЌШєAB=PCЃЌBP=DCЃЌЁЯDFE=45Ёу.
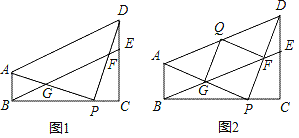
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКЫФБпаЮABEDЮЊЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌАбЁїPFGбиFGЗелЃЌЕУЕНЁїQFGЃЈЕуPгыЕуQЮЊЖдгІЕуЃЉЃЌЕуQдкADЩЯЃЌдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГіЭМжаЫљгаЕФЦНааЫФБпаЮЃЈВЛАќРЈЦНааЫФБпаЮABEDЃЌЕЋАќРЈЬиЪтЕФЦНааЫФБпаЮЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЬт
ЃЈ1ЃЉМЦЫуЃК|Љ ![]() |+ЃЈ
|+ЃЈ ![]() ЃЉЉ1Љ2cos45ЁуЃЎ
ЃЉЉ1Љ2cos45ЁуЃЎ
ЃЈ2ЃЉНтЗНГЬЃК ![]() +
+ ![]() =1ЃЎ
=1ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊТњзуЪаГЁашЧѓЃЌаТЩњЛюГЌЪадкЖЫЮчНкЧАЯІЙКНјМлИёЮЊ3дЊ/ИіЕФФГЦЗХЦєезгЃЌИљОнЪаГЁдЄВтЃЌИУЦЗХЦєезгУПИіЪлМл4дЊЪБЃЌУПЬьФмГіЪл500ИіЃЌВЂЧвЪлМлУПЩЯеЧ0.1дЊЃЌЦфЯњЪлСПНЋМѕЩй10ИіЃЌЮЊСЫЮЌЛЄЯћЗбепРћвцЃЌЮяМлВПУХЙцЖЈЃЌИУЦЗХЦєезгЪлМлВЛФмГЌЙ§НјМлЕФ200%ЃЌЧыФуРћгУЫљбЇжЊЪЖАяжњГЌЪаИјИУЦЗХЦєезгЖЈМлЃЌЪЙГЌЪаУПЬьЕФЯњЪлРћШѓЮЊ800дЊЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
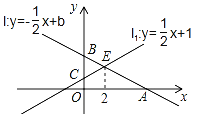
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпlЃКy=Љ![]() x+bгыxжсЃЌyжсЕФНЛЕуЗжБ№ЮЊAЃЌBЃЌжБЯпl1ЃКy=
x+bгыxжсЃЌyжсЕФНЛЕуЗжБ№ЮЊAЃЌBЃЌжБЯпl1ЃКy=![]() x+1гыyжсНЛгкЕуCЃЌжБЯпlгыжБЯпllЕФНЛЕуЮЊEЃЌЧвЕуEЕФКсзјБъЮЊ2ЃЎ
x+1гыyжсНЛгкЕуCЃЌжБЯпlгыжБЯпllЕФНЛЕуЮЊEЃЌЧвЕуEЕФКсзјБъЮЊ2ЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§bЕФжЕКЭЕуAЕФзјБъЃЛ
ЃЈ2ЃЉЩшЕуDЃЈaЃЌ0ЃЉЮЊxжсЩЯЕФЖЏЕуЃЌЙ§ЕуDзїxжсЕФДЙЯпЃЌЗжБ№НЛжБЯпlгыжБЯпllгкЕуMЁЂNЃЌШєвдЕуBЁЂOЁЂMЁЂNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧѓaЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвЛТьвЯДгдЕуOГіЗЂЃЌАДЯђЩЯЁЂЯђгвЁЂЯђЯТЁЂЯђгвЕФЗН
ЯђвРДЮВЛЖЯвЦЖЏЃЌУПДЮвЦЖЏ1ИіЕЅЮЛЃЌЦфаазпТЗЯпШчЯТЭМЫљЪОЃЎ

(1)ЬюаДЯТСаИїЕуЕФзјБъЃКA4( ЃЌ )ЁЂA8( ЃЌ )ЁЂA12( ЃЌ )ЃЛ
(2)аДГіЕуA4nЕФзјБъ(nЪЧе§ећЪ§)ЃЛ
(3)жИГіТьвЯДгЕуA100ЕНЕуA101ЕФвЦЖЏЗНЯђЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com