
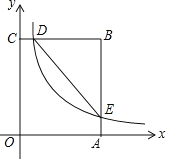
【题目】如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=![]() (k>0)的图象经过点D且与边BA交于点E,连接DE.
(k>0)的图象经过点D且与边BA交于点E,连接DE.
(1)连接OE,若△EOA的面积为3,则k=___________;
(2)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
【答案】(1)6;(2)存在,D(![]() ,5).
,5).
【解析】分析:(1)连接OE,根据反比例函数k的几何意义,即可求出k的值.(2)根据矩形的长和宽及反比例函数y=![]() (k>0)表示D和E的坐标,计算tan∠BDE=tan∠CB′B的值相等,所以计算B′C的长,得出D的坐标.
(k>0)表示D和E的坐标,计算tan∠BDE=tan∠CB′B的值相等,所以计算B′C的长,得出D的坐标.
本题解析:
(1)连接OE,如图1,
∵Rt△AOE的面积为3,
∴k=2×3=6.
故答案为:6;
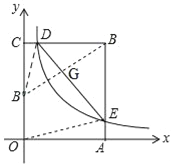
(2)连接DB′,
设D(![]() ,5),E(3,
,5),E(3,![]() ),
),
∴BD=3﹣![]() ,BE=5﹣
,BE=5﹣![]() ,
,
∴tan∠BDE=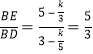 ,
,
∵B与B′关于DE对称,
∴DE是BB′的中垂线,
∴BB′⊥DE,BG=B′G,DB′=BD,
∴∠DGB=90°,
∴∠BDE+∠DBB′=90°,
∠CB′B+∠DBB′=90°,
∴∠BDE=∠CB′B,
∴tan∠BDE=tan∠CB′B=![]() =
=![]() =
=![]() ,
,
∴CB′=![]() ,
,
设CD=x,则BD=B′D=3﹣x,
则![]() ,
,
∴x=![]() ,
,
∴D(![]() ,5).
,5).


科目:初中数学 来源: 题型:
【题目】(1)在如图所示的数轴上,把数﹣2, ![]() ,4,﹣
,4,﹣![]() ,2.5表示出来,并用“<“将它们连接起来;
,2.5表示出来,并用“<“将它们连接起来;
(2)假如在原点处放立一挡板(厚度不计),有甲、乙两个小球(忽略球的大小,可看作一点),小球甲从表示数﹣2的点处出发,以1个单位长度/秒的速度沿数轴向左运动;同时小球乙从表示数4的点处出发,以2个单位长度/秒的速度沿数轴向左运动,在碰到挡板后即刻按原来的速度向相反的方向运动,设运动的时间为t(秒).
请从A,B两题中任选一题作答.
A.当t=3时,求甲、乙两小球之间的距离.
B.用含t的代数式表示甲、乙两小球之间的距离.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
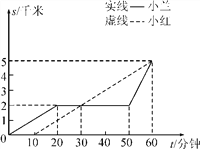
【题目】小红与小兰从学校出发到距学校5千米的书店买书,如图反应了他们两人离开学校的路程与时间的关系.请根据图形解决问题.
(1)小红与小兰谁先出发?早出发几分钟?
(2)小兰前20分钟的速度和最后10分钟的速度各是多少?
(3)小红与小兰从学校到书店的平均速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
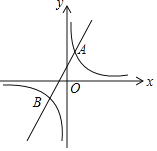
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,我区正在实施的“同城一体化”工程进展顺利区招投标中心在对观光路工程招标时,接到甲、乙两个工程队的投标书,甲、乙施工一天的工程费用分别为1.5万元和1.1万元,区招投标中心根据甲、乙两队的投标书测算,应有三种施工方案:
(1)甲队单独做这项工程刚好如期完成;
(2)乙队单独做这项工程,要比规定日期多5天;
(3)若甲、乙两队合作4天后,余下的工程由乙队单独做,也正好如期完成.
在确保如期完成的情况下,你认为哪种方案最节省工程款,通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中,OA、OB是半径,且OA=4,∠AOB=120°.点P是弧AB上的一个动点,连接AP、BP,分别作OC⊥PA,OD⊥PB,垂足分别为C、D,连接CD.
(1)如图①,在点P的移动过程中,线段CD的长是否会发生变化?若不发生变化,请求出线段CD的长;若会发生变化,请说明理由;
(2)如图②,若点M、N为![]() 的三等分点,点I为△DOC的外心.当点P从点M运动到N点时,点I所经过的路径长为__________.(直接写出结果)
的三等分点,点I为△DOC的外心.当点P从点M运动到N点时,点I所经过的路径长为__________.(直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
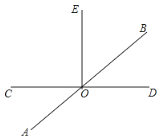
【题目】如图,已知直线AB和CD相交于点O,在∠COB的内部作射线OE.
(1)若∠AOC=36°,∠COE=90°,求∠BOE的度数;
(2)若∠COE:∠EOB:∠BOD=4:3:2,求∠AOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元,为了减少库存,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低( )元.
A.0.2或0.3
B.0.4
C.0.3
D.0.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com