
| A. | 15元和18元 | B. | 15元和15元 | C. | 18元和15元 | D. | 18元和18元 |
分析 根据题意先计算出本周销售套餐12元和18元的份数,再根据中位数和众数的定义即可得出答案.
解答 解:12元的份数有500×20%=100(份),
18元的份数有500-100-180=220(份),
∵本周销售套餐共计500份,
∴所购买的盒饭费用的中位数是第250和251个数的平均数,
∴中位数是15元;
18元出现的次数最多,则众数是18元;
故选A.
点评 此题考查了众数与中位数,众数是一组数据中出现次数最多的数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若$\frac{\sqrt{x-1}}{x-2}$有意义,则有x≥1且x≠2 | B. | 勾股定理是a2+b2=c2 | ||
| C. | 夹在两条平行线间的线段相等 | D. | a0=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西47°方向,距A船26海里的海域,C船位于A船的北偏东58°方向,同时又位于B船的北偏东88°方向.
某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西47°方向,距A船26海里的海域,C船位于A船的北偏东58°方向,同时又位于B船的北偏东88°方向.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
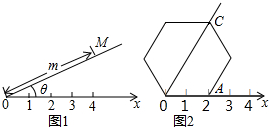
| A. | (60°,4) | B. | (45°,4) | C. | (60°,2) | D. | (50°,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com