
| ����ؿ���֪ ��a��������20�����ڣ���20�ţ���ÿ�źؿ�20Ԫ�� ��b��������20�����ϣ������ؿ����ռ۸�ȫ���������ۣ� |
���� ��1�������ܼ�=���ۡ���������ʽ���㼴�ɣ�
��2����С�������ķ���ΪyԪ����0��x��20��x��20��������ҳ�y����x�Ĵ���ʽ������ý⣻
��3�����������20��21�źؿ�����Ǯ����������360Ԫ���бȽϼ��ɵó�С���˴ι���ؿ��������ܶ���21Ҳ��������20����y=360���루2���Ĺ�ϵʽ�м��ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ�
��� �⣺��1��20��15=300��Ԫ����
�����С��ֻ��15�ţ�����ؿ�����ȥ300ԪǮ��
��2����С�������ķ���ΪyԪ��
���������֪����0��x��20ʱ��y=20x��
��x��20ʱ��y=0.75��20x=15x��
��С�������ķ���y=$\left\{\begin{array}{l}{20x��0��x��20��}\\{15x��x��20��}\end{array}\right.$��
��3����20��20=400��Ԫ����21��15=315��Ԫ����315��360��400��
��������ؿ���ȥ360Ԫ����С���˴ι���ؿ��������ܶ���21Ҳ��������20��
�൱y=360ʱ����20x=360��15x=360��
��ã�x=18��x=24��
�����С���˴ι���ȥ360Ԫ�����ʹ���ؿ�����Ϊ18��24�ţ�
���� ���⿼����һԪһ�η��̵�Ӧ���Լ��д���ʽ������Ĺؼ��ǣ���1�������ܼ�=���ۡ�������ʽ���㣻��2����0��x��20��x��20��������ҳ�y����x�Ĵ���ʽ����3����y=360���루2���Ľ�����ҳ�����x��һԪһ�η��̣�


 �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
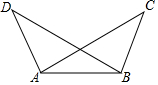 ��ͼ����ABC�ա�BAD��A��B��C��D�Ƕ�Ӧ���㣬���AB=5��BD=6��AD=4����ôBC���ڣ�������
��ͼ����ABC�ա�BAD��A��B��C��D�Ƕ�Ӧ���㣬���AB=5��BD=6��AD=4����ôBC���ڣ�������| A�� | 4 | B�� | 6 | C�� | 5 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 25 | B�� | 16 | C�� | 9 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
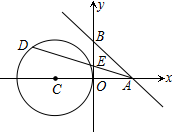 ��ͼ����ƽ��ֱ������ϵxOy�У�A��2��0����B��0��2����C��Բ��Ϊ��C��-2��0�����뾶Ϊ2����D��C��һ���㣬�߶�DA��y�ύ�ڵ�E�����ABE�����s��ȡֵ��Χ��2-$\frac{2\sqrt{3}}{3}$��S��2+$\frac{2\sqrt{3}}{3}$��
��ͼ����ƽ��ֱ������ϵxOy�У�A��2��0����B��0��2����C��Բ��Ϊ��C��-2��0�����뾶Ϊ2����D��C��һ���㣬�߶�DA��y�ύ�ڵ�E�����ABE�����s��ȡֵ��Χ��2-$\frac{2\sqrt{3}}{3}$��S��2+$\frac{2\sqrt{3}}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����PΪ������ABCD�ĶԽ���BD����һ�㣬����P��PE��BC��PF��CD������ֱ�Ϊ��E��F������EF�����н��ۢ١�FPD�ǵ���ֱ�������Σ���AP=EF����AD=PD���ܡ�PFE=��BAP��������ȷ�Ľ����Ǣ٢ڢܣ�������ţ�
��ͼ����PΪ������ABCD�ĶԽ���BD����һ�㣬����P��PE��BC��PF��CD������ֱ�Ϊ��E��F������EF�����н��ۢ١�FPD�ǵ���ֱ�������Σ���AP=EF����AD=PD���ܡ�PFE=��BAP��������ȷ�Ľ����Ǣ٢ڢܣ�������ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com