
����Ŀ����ͼ1����֪���Ϊ12�ij�����ABCD��һ��AB�������ϡ���A��ʾ����Ϊ��2����B��ʾ����Ϊ1������P�ӵ�B��������ÿ��1����λ���ȵ��ٶ����������������˶������P�˶�ʱ��Ϊt��t>0����.

��1�������εı�AD��Ϊ ��λ���ȣ�
��2����������ADP���Ϊ3ʱ����P���������ϱ�ʾ�����Ƕ��٣�
��3����ͼ2��������Q��ÿ��3����λ���ȵ��ٶȣ��ӵ�A���������������˶�����P�����ʱ����ͬ����ô��������BDQ��������BPC�������֮��Ϊ![]() ʱ��ֱ��д���˶�ʱ��t ��ֵ.
ʱ��ֱ��д���˶�ʱ��t ��ֵ.
���𰸡���1��4����2����3.5��0.5����3��t��ֵΪ![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��������
��1�������AB�ij����ɳ�����ABCD�����Ϊ12���������AD�ij���
��2����������ADP���Ϊ3�����AP�ij���Ȼ�������������ۣ��ٵ�P�ڵ�A����ߣ��ڵ�P�ڵ�A���ұߣ�
��3�� ������������ۣ�����Q��B����ߣ���BQ= 3-3t����|S��BDQ��S��BPC |=![]() ���ⷽ�̼��ɣ�����Q��B���ұߣ���BQ= 3t��3����|S��BDQ��S��BPC |=
���ⷽ�̼��ɣ�����Q��B���ұߣ���BQ= 3t��3����|S��BDQ��S��BPC |=![]() ���ⷽ�̼��ɣ�
���ⷽ�̼��ɣ�
��1��AB=1������2��=3��
�߳�����ABCD�����Ϊ12����AB��AD=12����AD=12��3=4��
�ʴ�Ϊ��4��
��2��������ADP�����![]() APAD=
APAD=![]() AP��4=3��
AP��4=3��
��ã�AP=1.5��
��P�ڵ�A����ߣ�-2-1.5=-3.5��P ���������ϱ�ʾ-3.5��
��P�ڵ�A���ұߣ�-2+1.5=-0.5��P ���������ϱ�ʾ-0.5��
����������P ���������ϱ�ʾ-3.5��-0.5��
��3��������������ۣ�����Q��B����ߣ���BQ=AB��AQ=3-3t��
S��BDQ=![]() BQAD=
BQAD=![]() =
=![]() ��S��BPC=
��S��BPC=![]() BPAD=
BPAD=![]() =
=![]() ��
��
![]() ��
��![]() ����ã�t=
����ã�t=![]() ��
��
����Q��B���ұߣ���BQ=AQ��AB=3t��3��
S��BDQ=![]() BQAD=
BQAD=![]() =
=![]() ��S��BPC=
��S��BPC=![]() BPAD=
BPAD=![]() =
=![]() ��
��
![]() ��
��![]() ����ã�t=
����ã�t=![]() ��
��![]() ��
��
����������t��ֵΪ![]() ��
��![]() ��
��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������A1A2A3A4,A5A6A7A8,A9A10A11A12,��(ÿ�������δӵ������Ķ��㿪ʼ,��˳ʱ�뷽��˳��,���μ�ΪA1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;��)�����ľ�������ԭ��O,���߾���x���y��ƽ��,�����ǵı߳�������2,4,6,��,��A20������Ϊ (����)
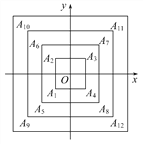
A. (5,5) B. (5,-5) C. (-5,5) D. (-5,-5)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ����������ABCD��������CGEF�У���B��C��G��ͬһ��ֱ���ϣ�M���߶�AE���е㣬DM���ӳ��߽�EF�ڵ�N������FM����֤��DM=FM��DM��FM������д֤�����̣�
��1����ͼ2������B��C��F��ͬһ��ֱ���ϣ�DM���ӳ��߽�EG�ڵ�N�������������䣬��̽���߶�DM��FM�������Ĺ�ϵ����д�����룬������֤����
��2����ͼ3������E��B��C��ͬһ��ֱ���ϣ�DM���ӳ��߽�CE���ӳ����ڵ�N�������������䣬̽���߶�DM��FM�������Ĺ�ϵ����ֱ��д�����룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ľ�����Ϊÿ��30Ԫ��Ϊ�˺������ۣ���Ͷ���г����������г����飬���ۼ�Ϊÿ��40Ԫʱ��ÿ�ܵ���������180���������ۼ�ÿ����1Ԫ����ÿ�ܵ��������ͻ����5������ÿ����Ʒ�����ۼ�����xԪ��ÿ�ܵ���������ΪyԪ��
��1���ú�x�Ĵ���ʽ��ʾ��ÿ����Ʒ�����ۼ�Ϊ�� ��Ԫ��ÿ����Ʒ������Ϊ�� ��Ԫ��ÿ�ܵ���Ʒ������Ϊ�� ������
��2����y����x�ĺ�����ϵʽ����Ҫ��д��x��ȡֵ��Χ����
��3��Ӧ����ȷ�����ۼۣ�ʹ����Ʒ��ÿ���������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������⼰��������գ�
��ͼ��ʾ��AB=10cm��DΪAC���е㣬DC=2cm��BE=![]() BC����CE�ij���
BC����CE�ij���
![]()
�⣺��ΪDΪAC���е㣬DC=2cm.
����AC="_______DC=_______" cm.
��ͼ��֪��BC="______" -AC
="10" cm-____cm
=_______cm.
����BE=![]() BC=______cm.
BC=______cm.
����CE=BC-BE=_____cm.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��ӡˢһ��֤�飬��������ӡˢ���ɹ�ѡ���׳��շѷ�ʽ�����ư��1000Ԫ��ÿ��ӡˢ��0.5Ԫ���ҳ��շѷ�ʽ�������ư�ѣ�ÿ����ӡˢ��1.5Ԫ������Уӡ��֤��x��.
��1����ӡ��֤��3000��ʱ���׳����շ�Ϊ Ԫ���ҳ����շ�Ϊ Ԫ��
��2������ӡˢ���ٱ�֤��ʱ�����������շ���ͬ��
��3������Ϊѡ����һ��ӡˢ�����Żݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AD��BC����ABC=90����
(1)ֱ����գ���BAD=______��.
(2)��P��CD�ϣ�����AP��AMƽ�֡�DAP��ANƽ�֡�PAB��AM��AN�ֱ�������BP���ڵ�M��N�����DAM=������
�����BAN�Ķ���(�ú����Ĵ���ʽ��ʾ)��
����AN��BM����̽����AMB�Ķ����Ƿ�Ϊ��ֵ����Ϊ��ֵ��������ö�ֵ������Ϊ��ֵ���������Ĵ���ʽ��ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��x����2�����У����������̵Ľ⣮
A.5x+7��7��2xB.6x��8��8x��4C.3x��2��4+xD.![]() x+2��6
x+2��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ڼס������̳�����ͬһ����Ʒ����õ�����ֱ�Ϊ![]() ��(��λ��Ԫ)��
��(��λ��Ԫ)��![]() ��������
��������![]() (��λ����)�ĺ�����ϵͼ����ͼ��ʾ���Ը���ͼ�����������⣺
(��λ����)�ĺ�����ϵͼ����ͼ��ʾ���Ը���ͼ�����������⣺

(1)�ֱ����![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
(2)�ֳ��ҷ������Ʒ800�������̳���400�������̳������ס������̳�����������Ʒ���ҿɻ�����������Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com