
【题目】如图,抛物线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,其中
两点,其中![]() 、
、![]() 是方程的
是方程的![]() 两根,且
两根,且![]() .
.
(![]() )求抛物线的解析式;
)求抛物线的解析式;
(![]() )直线
)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形.若存在,求所有
为直角三角形.若存在,求所有![]() 点坐标;反之说理;
点坐标;反之说理;
(![]() )点
)点![]() 为
为![]() 轴上方的抛物线上的一个动点(
轴上方的抛物线上的一个动点(![]() 点除外),连
点除外),连![]() 、
、![]() ,若设
,若设![]() 的面积为
的面积为![]() .
. ![]() 点横坐标为
点横坐标为![]() ,则
,则![]() 在何范围内时,相应的点
在何范围内时,相应的点![]() 有且只有
有且只有![]() 个.
个.

【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)解方程求得抛物线与x轴交点的横坐标,再用待定系数法求抛物线的解析式即可;(2)用待定系数法求得直线AC的解析式,再分①∠DBC=90°、②∠DBC=90°两种情况求点D的坐标即可;(3)求得点P在抛物线AB段上时S的最大值,再求得点P在抛物线AC段上时,S的最大值,即可得S的取值范围.
试题解析:
(![]() )
)![]() ,
,
![]() ,
, ![]() ,
,
设![]() ,
,
把![]() 代入得,
代入得, ![]() ,
,
解得![]() .
.
∴![]()
![]() .
.
(![]() )设直线AC的解析式为y=kx+b,将A、C两点坐标代入得,
)设直线AC的解析式为y=kx+b,将A、C两点坐标代入得,
![]() ,
,
解得 ,k=![]() ,b=4 ,
,b=4 ,
∴![]() .
.
①∠BDC=90°时,
![]() .
.
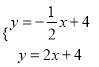 ,
, ![]() ,
,
∴![]() .
.
②∠DBC=90°时,x=-2,y=-![]() ×(-2)+4=5,则D点坐标为(-2,5);
×(-2)+4=5,则D点坐标为(-2,5);
∴![]() ,
, ![]() .
.

(3)点P在抛物线AC段上时S最大值为16,点P在抛物线AB段上时S最大值为20,
则S的取值范围为16<S<20.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 重合),延长
重合),延长![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)填空:
①当![]() 的值为_______时,四边形
的值为_______时,四边形![]() 是矩形;
是矩形;
②当![]() 的值为______时,四边形
的值为______时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
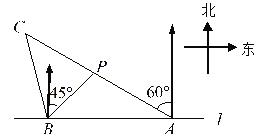
【题目】如图,在一笔直的海岸线![]() 上有
上有![]() 、
、![]() 两个观测站,
两个观测站,![]() 在
在![]() 的正东方向,
的正东方向,![]() (单位:
(单位:![]() )有一艘小船在点
)有一艘小船在点![]() 处,从
处,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向,从
的方向,从![]() 测得小船在北偏东
测得小船在北偏东![]() 的方向.(结果保留根号)
的方向.(结果保留根号)
(1)求点![]() 到海岸线
到海岸线![]() 的距离;
的距离;
(2)小船从点![]() 处沿射线
处沿射线![]() 的方向航行一段时间后,到达点
的方向航行一段时间后,到达点![]() 处,此时,从
处,此时,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向,求点
的方向,求点![]() 与点
与点![]() 之间的距离.
之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一副直角三角板(角度分别为30°、60°、90°和45°、45°、90°),如图(1)所示,其中一块三角板的直角边AC垂直于数轴,AC的中点过数轴原点O,AC=8,斜边AB交数轴于点G,点G对应数轴上的数是4;另一块三角板的直角边AE交数轴于点F,斜边AD交数轴于点H.
(1)如果△AGH的面积是10,△AHF的面积是8,则点F对应的数轴上的数是 ,点H对应的数轴上的数是 ;
(2)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,若∠HAO=a,试用a来表示∠M的大小:(写出推理过程)
(3)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,设∠EFH的平分线和
∠FOC的平分线交于点N,求∠N+∠M的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BE平分∠ABC,交AD于点E、F是BC上一点,且CF=AE,连接DF.
(1)求证:四边形BEDF是平行四边形;
(2)若∠ABC=70°,求∠CDF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() ,
,![]() ,试回答下列问题:
,试回答下列问题:
(1)如图1所示,求证:![]() .
.

(2)如图2,若点![]() 、
、![]() 在
在![]() 上,且满足
上,且满足![]() ,并且
,并且![]() 平分
平分![]() .求
.求![]() ________度.
________度.

(3)在(2)的条件下,若平行移动![]() ,如图3,那么
,如图3,那么![]() 的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.

(4)在(2)的条件下,如果平行移动![]() 的过程中,若使
的过程中,若使![]() ,求
,求![]() 度数.
度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:如图,∠ABC,射线BC上一点D.
求作:等腰△PBD,使线段BD为等腰△PBD的底边,点P在∠ABC内部,且点P到∠ABC两边的距离相等;

(2)在(1)的条件下,若∠ABC=60°,求等腰三角形△PBD顶角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com