
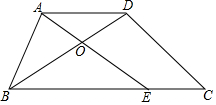
 如图,在梯形ABCD中,AB=AD=5cm,CD=6cm,BC=10cm,E是BC上的一个动点,当四边形AECD为平行四边形时,OA的长为3cm.
如图,在梯形ABCD中,AB=AD=5cm,CD=6cm,BC=10cm,E是BC上的一个动点,当四边形AECD为平行四边形时,OA的长为3cm. 科目:初中数学 来源: 题型:解答题
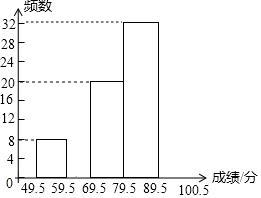 6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频数分布表和不完整的频数分布直方图如下:
6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频数分布表和不完整的频数分布直方图如下:| 分组 | 频数 | 所占百分比 |
| 49.5~59.5 | 8 | 8% |
| 59.5~69.5 | 12 | 12% |
| 69.5~79.5 | 20 | 20% |
| 79.5~89.5 | 32 | 32% |
| 89.5~100.5 | 28 | a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
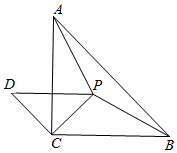 在等腰Rt△ABC中,∠ACB=90°,点P是△ABC内一点,且CP=$\sqrt{2}$,BP=AP=2,以点C为直角顶点,CP为直角边,作如图的等腰Rt△DCP,有如下4个结论:①点A与D的距离为2;②∠CPB=105°;③AB=$\sqrt{6}+\sqrt{2}$;④S△APB=2,其中正确的结论是( )
在等腰Rt△ABC中,∠ACB=90°,点P是△ABC内一点,且CP=$\sqrt{2}$,BP=AP=2,以点C为直角顶点,CP为直角边,作如图的等腰Rt△DCP,有如下4个结论:①点A与D的距离为2;②∠CPB=105°;③AB=$\sqrt{6}+\sqrt{2}$;④S△APB=2,其中正确的结论是( )| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ①② | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
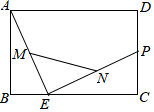 如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,点M、N分别是AE、PE的中点,则线段MN长为( )
如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,点M、N分别是AE、PE的中点,则线段MN长为( )| A. | 2$\sqrt{10}$ | B. | 3 | C. | $\sqrt{13}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com