
如图所示,在直角梯形ABCD中,AB为垂直于底边的腰,AD=1,BC=2,AB=3,点E为CD上异于C,D的一个动点,过点E作AB的垂线,垂足为F,△ADE,△AEB,△BCE的面积分别为S1,S2,S3.
(1)设AF=x,试用x表示S1与S3的乘积S1S3,并求S1S3的最大值;
(2)设 =t,试用t表示EF的长;
=t,试用t表示EF的长;
(3)在(2)的条件下,当t为何值时,S22=4S1S3.
解:(1)∵S1= AD•AF=
AD•AF= x,S3=
x,S3= BC•BF=
BC•BF= ×2×(3﹣x)=3﹣x,
×2×(3﹣x)=3﹣x,
∴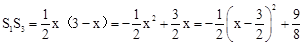 (0<x<3)。
(0<x<3)。
∴当x= 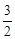 时,S1S3的最大值为
时,S1S3的最大值为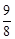 。
。
(2)如图,作DM⊥BC,垂足为M,DM与EF交与点N,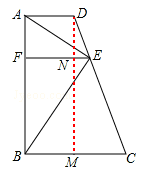
∵ =t,∴AF=tFB。
=t,∴AF=tFB。
∵△DNE∽△DMC ,BM=MC=AD=1,
∴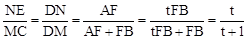 。∴NE=
。∴NE=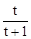 ,
,
∴EF=FN+NE=1+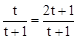 。
。
(3)∵AB=AF+FB=(t+1)FB=3,∴FB=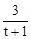 。∴AF=tFB=
。∴AF=tFB=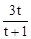 。
。
∴S1= AD•AF=
AD•AF= ×
×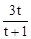 =
=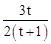 ,S3=
,S3= BC•FB=
BC•FB= ×2×
×2×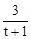 =
=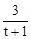 ,
,
S2= AB•FE=
AB•FE= ×3×
×3×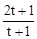 =
=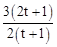 。
。
∴S1S3=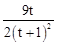 ,S22=
,S22=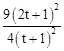 。
。
∴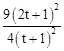 =4×
=4×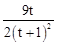 ,即4t2﹣4t+1=0,解得t=
,即4t2﹣4t+1=0,解得t= 。
。
∴当t= 时,S22=4S1S3。
时,S22=4S1S3。
解析试题分析:(1)直接根据三角形的面积公式解答即可。
(2)作DM⊥BC,垂足为M,DM与EF交与点N,根据 =t,可知AF=tFB,再由△DNE∽△DMC 和BM=MC=AD=1可得出
=t,可知AF=tFB,再由△DNE∽△DMC 和BM=MC=AD=1可得出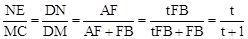 ,所以NE=
,所以NE=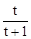 ,根据EF=FN+NE即可得出结论。
,根据EF=FN+NE即可得出结论。
(3)根据AB=AF+FB=(t+1)FB=3,可得出FB=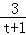 ,故可得出AF=tFB=
,故可得出AF=tFB=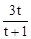 ,根据三角形的面积公式可用t表示出S1,S3,S2,由s22=4S1S3.即可得出t的值。
,根据三角形的面积公式可用t表示出S1,S3,S2,由s22=4S1S3.即可得出t的值。


科目:初中数学 来源: 题型:解答题
如图所示.某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上.其余两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,每平方米投资6元;在△BHE、△FCG上都种花,每平方米投资10元;在矩形EFGH上兴建爱心鱼池,每平方米投资4元.
(1)当FG长为多少米时,种草的面积与种花的面积相等?
(2)当矩形EFGH的边FG为多少米时,△ABC空地改造总投资最小,最小值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立。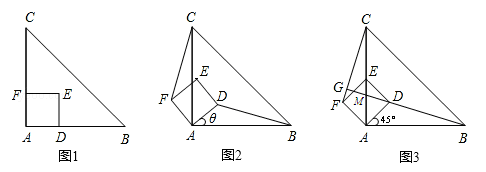
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由。
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G。
求证:BD⊥CF。
(3)在(2)小题的条件下, AC与BG的交点为M, 当AB=4,AD= 时,求线段CM的长。
时,求线段CM的长。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了测量旗杆AB的高度.甲同学画出了示意图1,并把测量结果记录如下,BA⊥EA于A,DC⊥EA于C,CD=a,CA=b,CE=c;乙同学画出了示意图2,并把测量结果记录如下,DE⊥AE于E,BA⊥AE于A,BA⊥CD于C,DE=m,AE=n,∠BDC=α.
(1)请你帮助甲同学计算旗杆AB的高度(用含a、b、c的式子表示);
(2)请你帮助乙同学计算旗杆AB的高度(用含m、n、α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
直角三角形ABC中,∠ABC=90°,AC=10,BC=6,AB=8。P是AC上的一个动点,当P在AC上运动时,设PC=x,△ABP 的面积为y.
(1)求AC边上的高是多少?
(2)求y与x之间的关系式。
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,贤贤同学用手工纸制作一个台灯灯罩,做好后发现上口太小了,于是他把纸灯罩对齐压扁,剪去上面一截后,正好合适,以下裁剪示意图中,正确的是( )
A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com