
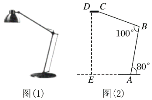
【题目】如图(1)是小明家购买的一款台灯,现忽略支架的粗细,得到它的侧面简化示意图如图(2)所示.支架AB与桌面的夹角为80°,支架AB与支架BC的夹角为100°,CD平行于桌面,支架AB,BC的长度均为20cm.求灯泡顶端D到桌面的距离DE.(结果精确到1cm.参考数据:sin80°≈0.98,cos80°≈0.17,tan80°≈5.67,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
【答案】26cm
【解析】
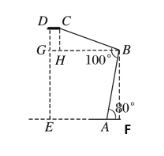
如图,过点B作BF⊥EA于点F,过点B作BG∥EA,交DE于点G,过点C作CH⊥BG于点H,先通过解直角三角形求出BF与CH的长,再通过四边形DCHG和四边形EFBG是矩形,求得DG与GE的长,即可求得灯泡顶端D到桌面的距离DE.
如图,过点B作BF⊥EA于点F,
过点B作BG∥EA,交DE于点G,过点C作CH⊥BG于点H.
∵在Rt△BAF中,AB=20cm,∠BAF=80°,
∴BF=ABsin∠BAF=20sin80°≈19.6(cm),
∵GB∥EF,
∴∠GBA=∠BAF=80°,
∴∠CBH=100°-80°=20°,
∵在Rt△BCH中,BC=20cm,∠CBH=20°,
∴CH=BCsin∠CBH=20sin20°≈6.8(cm)
∵四边形DCHG和四边形EFBG是矩形,
∴DG=CH=6.8cm,GE=BF=19.6cm,
∴DE=6.8+19.6=26.4≈26(cm) .
故灯泡顶端D到桌面的距离DE约为26cm.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知函数y1=x2+ax+1,y2=x2+bx+2,y3=x2+cx+4,其中a,b,c是正实数,且满足b2=ac.设函数y1,y2,y3的图象与x轴的交点个数分别为M1,M2,M3,( )
A.若M1=2,M2=2,则M3=0B.若M1=1,M2=0,则M3=0
C.若M1=0,M2=2,则M3=0D.若M1=0,M2=0,则M3=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=mx2+4mx﹣5m(m≠0),一次函数y2=2x﹣2,有下列结论:
①当x>﹣2时,y随x的增大而减小;
②二次函数y1=mx2+4mx﹣5m(m≠0)的图象与x轴交点的坐标为(﹣5,0)和(1,0);
③当m=1时,y1≤y2;
④在实数范围内,对于x的同一个值,这两个函数所对应的函数值y2≤y1均成立,则m![]() .
.
其中,正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
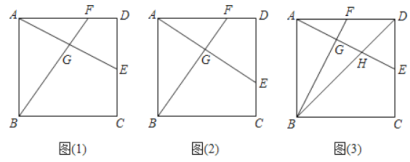
【题目】如图,正方形![]() 的边长为
的边长为![]() 分别是边
分别是边![]() 上的动点,
上的动点,![]() 和
和![]() 交于点
交于点![]() .
.
![]() 如图(1),若
如图(1),若![]() 为边
为边![]() 的中点,
的中点,![]() , 求
, 求![]() 的长;
的长;
![]() 如图(2),若点
如图(2),若点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,点
运动,点![]() 在
在![]() .上从
.上从![]() 向
向![]() 运动.两点同时出发,同时到达各自终点,求在运动过程中,点
运动.两点同时出发,同时到达各自终点,求在运动过程中,点![]() 运动的路径长:
运动的路径长:
![]() 如图(3), 若
如图(3), 若![]() 分别是边
分别是边![]() 上的中点,
上的中点,![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的正切值.
的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
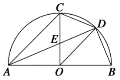
【题目】如图,AB是半圆O的直径,半径OC⊥AB于点O,点D是![]() 的中点,连接CD、OD、BD.下列四个结论:①AC∥OD;②CD=BD;③△ODE∽△CAE;④∠ADC=∠BOD.其中正确结论的序号是( )
的中点,连接CD、OD、BD.下列四个结论:①AC∥OD;②CD=BD;③△ODE∽△CAE;④∠ADC=∠BOD.其中正确结论的序号是( )
A.①②③④B.①②④C.②③D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
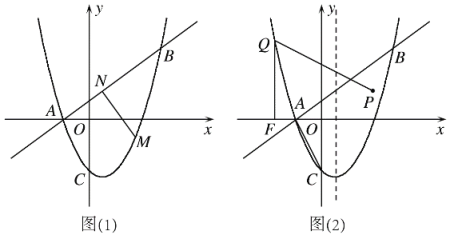
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),与y轴交于C(0,-2);直线![]() 经过点A且与抛物线交于另一点B
经过点A且与抛物线交于另一点B![]() .
.
(1)直接写出抛物线的解析式 ;
(2)如图(1),点M是抛物线上A,B两点间的任一动点,MN⊥AB于点N,试求出MN的最大值 ,并求出MN最大时点M的坐标;
(3)如图(2),连接AC,已知点P的坐标为(2,1),点Q为对称轴左侧的抛物线上的一动点,过点Q作QF⊥x轴于点F,是否存在这样的点Q,使得∠FQP=∠CAO.若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
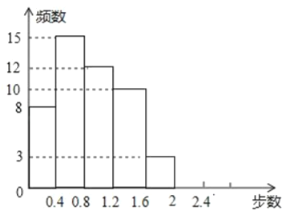
【题目】“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了某市![]() 名教师某日“微信运动”中的步数情况并进行统计整理,绘制了如下的统计图表(不完整) :请根据以上信息,解答下列问题
名教师某日“微信运动”中的步数情况并进行统计整理,绘制了如下的统计图表(不完整) :请根据以上信息,解答下列问题
![]() 写出
写出![]() 的值;
的值;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 若该市约有
若该市约有![]() 名教师,估计日行走步数超过
名教师,估计日行走步数超过![]() 万步(包含
万步(包含![]() 万步)的教师约有多少名?
万步)的教师约有多少名?
步数(万步) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
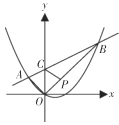
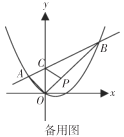
【题目】如图,在平面直角坐标系中,抛物线![]() 上有两点
上有两点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 到两坐标轴的距离相等.点
到两坐标轴的距离相等.点![]() 到两坐标轴的距离也相等.
到两坐标轴的距离也相等.
(1)求点![]() ,
,![]() 的坐标并直接写出
的坐标并直接写出![]() 的形状;
的形状;
(2)若点![]() 为线段
为线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,当
,当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标;
的坐标;
(3)若点![]() 为
为![]() 轴上一动点,当
轴上一动点,当![]() 是以
是以![]() 为斜边的直角三角形时,求点
为斜边的直角三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:径赛项目:100m,200m,![]() 分别用
分别用![]() 、
、![]() 、
、![]() 表示
表示![]() ;田赛项目:跳远,跳高
;田赛项目:跳远,跳高![]() 分别用
分别用![]() 、
、![]() 表示
表示![]() .
.
![]() 该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
![]() 该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com