
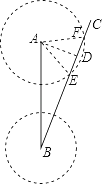
【题目】台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形气旋风暴,有极强的破坏力,此时某台风中心在海域B处,在沿海城市A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响. 试问:

(1)A城市是否会受到台风影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
【答案】(1)该城市会受到这次台风的影响;(2)16;(3)7.2.
【解析】
试题(1)过A作AD⊥BC于D,利用30°角所对边是斜边一半,求得AD,与200比较.(2) 以A为圆心,200为半径作⊙A交BC于E、F,勾股定理计算弦长EF.(3) AD距台风中心最近,计算风力级别.
试题解析:
(1)该城市会受到这次台风的影响. 理由是:如图,过A作AD⊥BC于D.在Rt△ABD中,
∵∠ABD=30°,AB=240,
∴AD= ![]() AB=120,
AB=120,
∵城市受到的风力达到或超过四级,则称受台风影响,
∴受台风影响范围的半径为25×(12﹣4)=200,
∵120<200,
∴该城市会受到这次台风的影响.
(2)如图以A为圆心,200为半径作⊙A交BC于E、F, 则AE=AF=200,
∴台风影响该市持续的路程为:EF=2DE=2 ![]() =320,
=320,
∴台风影响该市的持续时间t=320÷20=16(小时).
(3)∵AD距台风中心最近,
∴该城市受到这次台风最大风力为:12﹣(120÷25)=7.2(级).


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E. 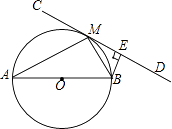
(1)求证:∠BME=∠MAB;
(2)求证:BM2=BEAB;
(3)若BE= ![]() ,sin∠BAM=
,sin∠BAM= ![]() ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计), 右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由两个正方形组成的长方形花坛ABCD,小明从顶点A沿着花坛间小路直到走到长边中点O,再从中点O走到正方形OCDF的中心![]() ,再从中心
,再从中心![]() 走到正方形
走到正方形![]() GFH的中点
GFH的中点![]() ,又从中心
,又从中心![]() 走到正方形
走到正方形![]() IHJ的中心
IHJ的中心![]() ,再从中心
,再从中心![]() 走到正方形
走到正方形![]() KJP的中心
KJP的中心![]() ,一共走了
,一共走了![]() m,则长方形花坛ABCD的周长是( )
m,则长方形花坛ABCD的周长是( )

A. 36m B. 48m C. 96m D. 60m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD∥BC,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动.
(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,且BE=3cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CBA=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与x轴交于点A,点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A,点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.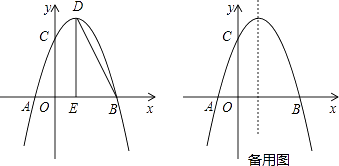
(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在平面内,以线段MN为对角线作正方形MPNQ,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长,交DC于点F,求证: 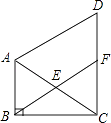
(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年5月9日﹣11日,贵州省第十一届旅游产业发展大会在准一市茅台镇举行,大会推出五条遵义精品旅游线路:A红色经典,B醉美丹霞,C生态茶海,D民族风情,E避暑休闲.某校摄影小社团在“祖国好、家乡美”主题宣传周里,随机抽取部分学生举行“最爱旅游路线”投票活动,参与者每人选出一条心中最爱的旅游路线,社团对投票进行了统计,并绘制出如下不完整的条形统计图和扇形统计图,请解决下列问题. 
(1)本次参与投票的总人数是人.
(2)请补全条形统计图.
(3)扇形统计图中,线路D部分的圆心角是度.
(4)全校2400名学生中,请你估计,选择“生态茶海”路线的人数约为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com