
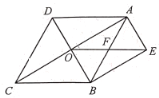
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=10,AC=16,求菱形ABCD的面积.
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣![]() >0的解集.
>0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则每个小正方形的边长为( )
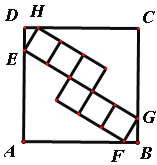
A.6 B.5 C.2![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
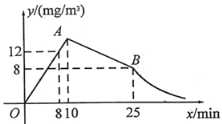
【题目】春季是流感高发的季节,为此,某校为预防流感,对教室进行熏药消毒.在对教室进行消毒的过程中,先经过10min的药物燃烧,再封闭教室15min,然后打开门窗进行通风.已知室内空气中含药量![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 之间的函数关系式如图所示(即图中线段OA、线段AB和双曲线在点B及其右侧部分),请根据图中信息解答下列问题:
之间的函数关系式如图所示(即图中线段OA、线段AB和双曲线在点B及其右侧部分),请根据图中信息解答下列问题:
(1)求药物燃烧阶段和打开门窗进行通风阶段![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)若室内空气中的含药量不低于![]() 且持续时间不少于35min,才能有效消灭病毒,则此次消毒是否有效?请说明理由.
且持续时间不少于35min,才能有效消灭病毒,则此次消毒是否有效?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)用方程解答下列问题
(1)一个角的余角比它的补角的![]() 还少15°,求这个角的度数.
还少15°,求这个角的度数.
(2)几个人共同搬运一批货物,如果每人搬运8箱货物,则剩下7箱货物未搬运;如果每人搬运12箱货物,则缺13箱货物,求参与搬运货物的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
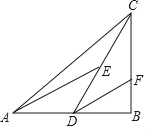
【题目】定义:有两条边长的比值为![]() 的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
(1)设“潜力三角形”较短直角边长为a,斜边长为c,请你直接写出![]() 的值为 ;
的值为 ;
(2)若∠AED=∠DCB,求证:△BDF是“潜力三角形”;
(3)若△BDF是“潜力三角形”,且BF=1,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1∶![]() ,AB=10米,AE=15米(i=1∶
,AB=10米,AE=15米(i=1∶![]() 是指坡面的铅直高度BH与水平长度AH的比).
是指坡面的铅直高度BH与水平长度AH的比).

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com