
 ��ͼ��1�����ı���ABCD��һ�ű߳�Ϊ2a��������ֽƬ���Ƚ�������ABCD���ۣ�ʹBC��AD�غϣ��ۺ�ΪEF�������������չƽ��Ȼ����ֱ��CG�۵���ʹ��B����EF�ϣ���Ӧ��ΪB�䣮
��ͼ��1�����ı���ABCD��һ�ű߳�Ϊ2a��������ֽƬ���Ƚ�������ABCD���ۣ�ʹBC��AD�غϣ��ۺ�ΪEF�������������չƽ��Ȼ����ֱ��CG�۵���ʹ��B����EF�ϣ���Ӧ��ΪB�䣮���� ��1�������۵������ʣ�CB��=BC=2a��CF=a�������CB��F=30�㣬�ٸ���ͬ�ǵ������ȵó���EGB��=30�㣻
��2����Rt��CFB���У���֪B��F=$\sqrt{3}$a��EB��=2a-$\sqrt{3}$a����GB��=x����EG=a-x����Rt��EGB���У����ݹ��ɶ����з�����⣬Ȼ��������ж�����㼴�ɣ�
��3������AB������������ȫ�ȼ��Գ��Եó�EB��=NP=FD��=MQ�������ζ��ۿɵã�OE=ON=OF=OM��OB��=OP=0D��=OQ���ı���B��PD��QΪ���Σ��ɶ���֪��MN��EF���ڵ�O��PQ��B��D���ڵ�0���õ��ı���B��PD��QΪ�����Σ���PB��=$\frac{1}{2}$CG�����ݹ��ɶ������CG����������ı���B��PD��Q�������
��� �⣺��1�������۵������ʣ�CB��=BC=2a��CF=a��
��$\frac{CF}{CB��}=\frac{1}{2}$
���CB��F=30�㣬
�ߡ�GB��C=90�㣬
���EGB��=30�㣻
��2����ͼ1����Rt��CFB���У���֪B��F=$\sqrt{3}$a��
��EB��=2a-$\sqrt{3}$a��
��GB��=x����EG=a-x��
��x2=��a-x��2+��2a-$\sqrt{3}$a��2��
��ã�x=��4-2$\sqrt{3}$��a��
��Rt��CGB����
tan��B��CG=$\frac{GB��}{CB��}=\frac{��4-2\sqrt{3��}a}{2a}$=2-$\sqrt{3}$��
֤������ͼ2������AB��
�ɣ�2����֪��B��AE=��GCB�䣬���۵���֪����GCB��=��PCN��
���B��AE=��PCN��
�ɶ���֪��AEB��=��CNP=90�㣬AE=$\frac{1}{2}$ AB��CN=$\frac{1}{2}$ BC��
�֡��ı���ABCD�������Σ�
��AB=BC��
��AE=CN��
�ڡ�AEB��͡�CNP�У�
$\left\{\begin{array}{l}{��B��AE=��PCN}\\{AE=CN}\\{��AEB��=��CNP}\end{array}\right.$��
���AEB��ա�CNP��ASA����
��EB��=NP��
ͬ���ɵã�EB��=MQ��
�ɶԳ��Կ�֪��EB��=FD�䣬
��EB��=NP=FD��=MQ��
�����ζ��ۿɵã�OE=ON=OF=OM��
��OB��=OP=0D��=OQ��
���ı���B��PD��QΪ���Σ�
�ɶ���֪��MN��EF���ڵ�O��
��PQ��B��D���ڵ�0��
���ı���B��PD��QΪ�����Σ�
�����۵�������֪��PΪCG���е㣬
��PB��=$\frac{1}{2}$CG��
��CG2=BG2+CB2=[��4-2$\sqrt{3}$��a]2+��2a��2=��32-16$\sqrt{3}$��a2��
���ı���B��PD��Q�����=PB��2=��$\frac{1}{2}$CG��2=$\frac{1}{4}$����32-16$\sqrt{3}$��a2=��8-$\sqrt{3}$��a2��
���� ������Ҫ�������ı��ε��ۺ��⣬�������Ĺؼ��������ۺ����Ƚǣ���ȱߣ������3С��Ĺؼ���֤���ı���B��PD��Q�������Σ�


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��OCƽ�֡�AOD��ODƽ�֡�BOC�����н��۲��������ǣ�������
��ͼ��OCƽ�֡�AOD��ODƽ�֡�BOC�����н��۲��������ǣ�������| A�� | ��AOC=��BOD | B�� | ��COD=$\frac{1}{2}$AOB | C�� | ��AOC=$\frac{1}{2}$��AOD | D�� | ��BOC=2��BOD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
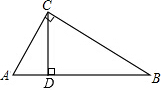 ��ͼ����ACB=90�㣬CD��AB��D��������Ľ����У���ȷ���ǣ�������
��ͼ����ACB=90�㣬CD��AB��D��������Ľ����У���ȷ���ǣ�������| A�� | �٢� | B�� | �٢� | C�� | �ۢ� | D�� | �ܢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
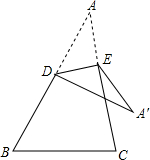 ��ͼ���ڡ�ABC�У���DE�۵�����A�������������ڵ�ƽ���ڵĵ�ΪA1������A=30�㣬��BDA1=80�㣬���CEA1�Ķ���Ϊ20�㣮
��ͼ���ڡ�ABC�У���DE�۵�����A�������������ڵ�ƽ���ڵĵ�ΪA1������A=30�㣬��BDA1=80�㣬���CEA1�Ķ���Ϊ20�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
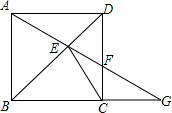 ��ͼ����������ABCD�Խ���������ȡ��E��AE�ӳ��߽�CD��F����BC�ӳ�����G����֤��EC2=EF•EG��
��ͼ����������ABCD�Խ���������ȡ��E��AE�ӳ��߽�CD��F����BC�ӳ�����G����֤��EC2=EF•EG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
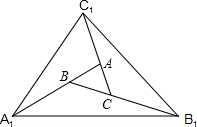 ��ͼ�������Ϊ1�ġ�ABC��ν������²�������һ�β������ֱ��ӳ�AB��BC��CA����A1��B1��C1��ʹ��A1B=AB��B1C=BC��C1A=CA��˳������A1��B1��C1���õ���A1B1C1���������ΪS1���ڶ��β������ֱ��ӳ�A1B1��B1C1��C1A1��A2��B2��C2��ʹ��A2B1=A1B1��B2C1=B1C1��C2A1=C1A1��˳������A2��B2��C2���õ���A2B2C2���������ΪS2�������˹��ɼ�����ȥ����n�β����õ���AnBnCn����S1=7����AnBnCn�����Sn=7n��
��ͼ�������Ϊ1�ġ�ABC��ν������²�������һ�β������ֱ��ӳ�AB��BC��CA����A1��B1��C1��ʹ��A1B=AB��B1C=BC��C1A=CA��˳������A1��B1��C1���õ���A1B1C1���������ΪS1���ڶ��β������ֱ��ӳ�A1B1��B1C1��C1A1��A2��B2��C2��ʹ��A2B1=A1B1��B2C1=B1C1��C2A1=C1A1��˳������A2��B2��C2���õ���A2B2C2���������ΪS2�������˹��ɼ�����ȥ����n�β����õ���AnBnCn����S1=7����AnBnCn�����Sn=7n���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com