
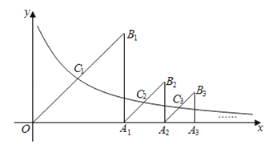
【题目】如图,△OA1B1,△A1A2B2,△A2A3B3,…是分别以A1,A2,A3,…为直角顶点,一条直角边在x轴正半轴上的等腰直角三角形,其斜边的中点C1(x1,y1),C2(x2,y2),C3(x3,y3),…均在反比例函数![]() (x>0)的图象上.则y1+y2+…+y8的值为( )
(x>0)的图象上.则y1+y2+…+y8的值为( )
A.![]() B.6C.
B.6C.![]() D.
D.![]()
【答案】C
【解析】
根据点C1的坐标,确定y1,可求反比例函数关系式,由点C1是等腰直角三角形的斜边中点,可以得到OA1的长,然后再设未知数,表示点C2的坐标,确定y2,代入反比例函数的关系式,建立方程解出未知数,表示点C3的坐标,确定y3,……然后再求和.
解:过C1、C2、C3…分别作x轴的垂线,垂足分别为D1、D2、D3…

其斜边的中点C1在反比例函数y=![]() ,
,
∴C1(2,2),即y1=2,
∴OD1=D1A1=2,
设A1D2=a,则C2D2=a 此时C2(4+a,a),代入y=![]() ,得:a(4+a)=4,
,得:a(4+a)=4,
解得:![]() ,即:y2=
,即:y2=![]() ;
;
同理:y3=![]() ;
;
y4=![]() ;
;
……
![]() ;
;
∴y1+y2+…+y8=![]()
=![]()
=![]()
=![]() ;
;
故选:C.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.
(1)等边三角形“內似线”的条数为 ;
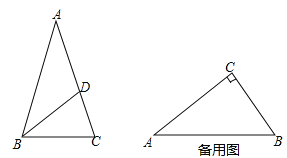
(2)如图,△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求证:BD是△ABC的“內似线”;
(3)在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别在边AC、BC上,且EF是△ABC的“內似线”,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
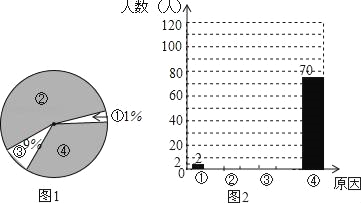
【题目】中国式过马路,是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关”针对这种现象某媒体记者在多个路口采访闯红灯的行人,得出形成这种现象的四个基本原因,①红绿灯设置不科学,交通管理混乱占1%;②侥幸心态;③执法力度不够占9%;④从众心理,该记者将这次调查情况整理并绘制了如下尚不完整的统计图,请根据相关信息,解答下列问题.
(1)该记者本次一共调査了 名行人;
(2)求图1中④所在扇形的圆心角,并补全图2;
(3)在本次调查中,记者随机采访其中的一名行人,求他属于第②种情况的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
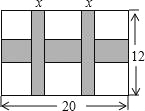
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点G,如图,当点G运动到某位置时,以AG,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点G的坐标;
(3)若抛物线上存在点P,使得△ACP是以AC为直角边的直角三角形,直接写出所有符合条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
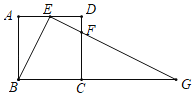
【题目】如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且∠BEF=90°,延长EF交BC的延长线于点G.
(1)求证:△ABE∽△EGB.
(2)若AB=4,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.
(1)求证:EM是⊙O的切线;
(2)若∠A=∠E,BC=![]() ,求阴影部分的面积.(结果保留
,求阴影部分的面积.(结果保留![]() 和根号).
和根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司共有![]() 三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求这个公司平均每人所创年利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为_____.
S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com