
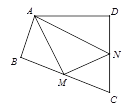
【题目】四边形ABCD中,∠B=∠D=90°,∠C=72°,在BC、CD上分别找一点M、N,使△AMN的周长最小时,∠AMN+∠ANM的度数为_______
【答案】144°
【解析】
根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″=60°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.
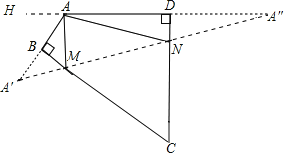
解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.
∵四边形ABCD中,∠B=∠D=90°,∠C=72°
∴∠DAB=108°,
∴∠AA′M+∠A″=72°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×72°=144°,
故填:144°.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元初,中美洲马雅人使用的一种数字系统与其他计数方式都不相同,它采用二十进位制但只有3个符号,用点“![]() ”、划“—”、卵形“
”、划“—”、卵形“![]() ”来表示我们所使用的自然数,如自然数1-19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
”来表示我们所使用的自然数,如自然数1-19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
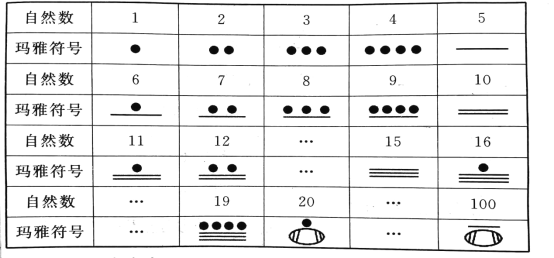
(1)玛雅符号![]() 表示的自然数是哪个数;
表示的自然数是哪个数;
(2)请你画出表示自然数280的玛雅符号.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴、y轴交于
分别与x轴、y轴交于![]() 两点,与直线
两点,与直线![]() 交于点C(4,2).
交于点C(4,2).
(1)点A坐标为( , ),B为( , );
(2)在线段![]() 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线![]() 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得![]() 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
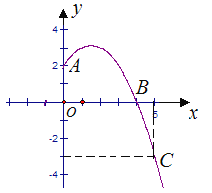
【题目】已知抛物线y=ax2+b x+c经过A,B,C三点,当x≥0时,其图象如图所示.
(1)求抛物线的解析式,写出抛物线的顶点坐标;
(2)画出抛物线y=ax2+b x+c当x<0时的图象;
(3)利用抛物线y=ax2+b x+c,写出x为何值时,y>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为原点,A. B为数轴上两点,AB=15,且OA:OB=2.
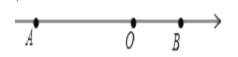
(1)A、B对应的数分别为___、___;
(2)点A. B分别以4个单位/秒和3个单位/秒的速度相向而行,则几秒后A. B相距1个单位长度?
(3)点A. B以(2)中的速度同时向右运动,点P从原点O以7个单位/秒的速度向右运动,是否存在常数m,使得4AP+3OBmOP为定值,若存在请求出m值以及这个定值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A .在函数y=-x2中,当x=0时y有最大值0
B.在函数y=2x2中,当x>0时y随x的增大而增大
C.抛物线y=2x2,y=-x2,![]() 中,抛物线y=2x2的开口最小,抛物线y=-x2的开口最大
中,抛物线y=2x2的开口最小,抛物线y=-x2的开口最大
D.不论a是正数还是负数,抛物线y=ax2的顶点都是坐标原点
查看答案和解析>>
科目:初中数学 来源: 题型:
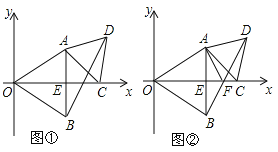
【题目】如图,△AOB和△ACD是等边三角形,其中AB⊥x轴于E点,点E坐标为(3,0),点C(5,0).
(1)如图①,求BD的长;
(2)如图②,设BD交x轴于F点,求证:∠OFA=∠DFA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面文字:
对于(﹣5![]() )+(﹣9
)+(﹣9![]() )+17
)+17![]() +(﹣3
+(﹣3![]() )
)
可以如下计算:
原式=[(﹣5)+(﹣![]() )]+[(﹣9)+(﹣
)]+[(﹣9)+(﹣![]() )]+(17+
)]+(17+![]() )+[(﹣3)+(﹣
)+[(﹣3)+(﹣![]() )]
)]
=[(一5)+(﹣9)+17+(一3)]+[(﹣![]() )+(﹣
)+(﹣![]() )+
)+![]() +(﹣
+(﹣![]() )]=0+(﹣1
)]=0+(﹣1![]() )
)
=﹣1![]()
上面这种方法叫拆项法,你看懂了吗?
仿照上面的方法,请你计算:(﹣1![]() )+(﹣2000
)+(﹣2000![]() )+4000
)+4000![]() +(﹣1999
+(﹣1999![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com