
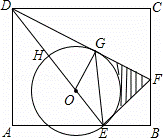
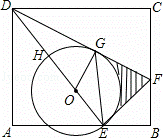
如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F
(1)求证:△ADE∽△BEF;
(2)设H是ED上一点,以EH为直径作⊙O,DF与⊙O相切于点G,若DH=OH=3,求图中阴影部分的面积(结果保留到小数点后面第一位,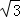 ≈1.73,π≈3.14).
≈1.73,π≈3.14).


(1)证明:∵四边形ABCD是矩形,
∴∠A=∠B=90°.
∵EF⊥DE,
∴∠DEF=90°.
∴∠AED=90°﹣∠BEF=∠EFB.
∵∠A=∠B,∠AED=∠EFB,
∴△ADE∽△BEF.
(2)解:∵DF与⊙O相切于点G,
∴OG⊥DG.
∴∠DGO=90°.
∵DH=OH=OG,
∴sin∠ODG=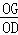 =
=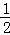 .
.
∴∠ODG=30°.
∴∠GOE=120°.
∴S扇形OEG=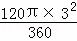 =3π.
=3π.
在Rt△DGO中,
cos∠ODG=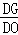 =
=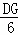 =
=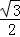 .
.
∴DG=3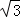 .
.
在Rt△DEF中,
tan∠EDF=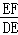 =
=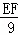 =
=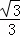 .
.
∴EF=3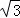 .
.
∴S△DEF=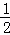 DE•EF=
DE•EF=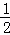 ×9×3
×9×3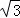 =
=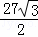 ,
,
S△DGO=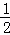 DG•GO=
DG•GO=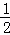 ×3
×3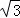 ×3=
×3=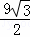 .
.
∴S阴影=S△DEF﹣S△DGO﹣S扇形OEG
=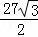 ﹣
﹣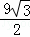 ﹣3π
﹣3π
=.9 ﹣3π
﹣3π
≈9×1.73﹣3×3.14
=6.15
≈6.2
∴图中阴影部分的面积约为6.2.




科目:初中数学 来源: 题型:
南宁东高铁火车站位于南宁市青秀区凤岭北路,火车站总建筑面积约为267000平方米,其中数据267000用科学记数法表示为  ( )
( )
(A)26.7×10 (B)2.67×10
(B)2.67×10 (C)2.67×10
(C)2.67×10 (D)0.267×10
(D)0.267×10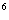


查看答案和解析>>
科目:初中数学 来源: 题型:
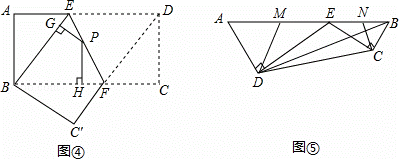
张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.
【变式探究】如图3,当点P在BC延长线上时,其余条件不变,求证:PD﹣PE=CF;
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】图5是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,且AD•CE=DE•BC,AB=2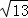 dm,AD=3dm,BD=
dm,AD=3dm,BD=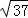 dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.
dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,M,N两点在数轴上表示的数分别是m,n,则下列式子中成立的是( )
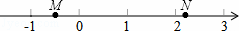
|
| A. | m+n<0 | B. | ﹣m<﹣n | C. | |m|﹣|n|>0 | D. | 2+m<2+n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com