
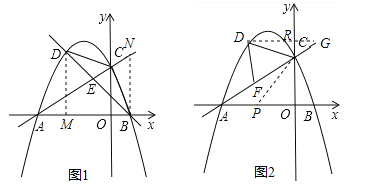
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļß![]() ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻß
ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻß![]() ¾¹żA”¢CĮ½µć£¬ÓėxÖįµÄĮķŅ»½»µćĪŖµćB£®
¾¹żA”¢CĮ½µć£¬ÓėxÖįµÄĮķŅ»½»µćĪŖµćB£®
£Ø1£©ĒóÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©µćDĪŖÖ±ĻßACÉĻ·½Å×ĪļĻßÉĻŅ»¶Æµć£»
¢ŁĮ¬½ÓBC”¢CD£¬ÉčÖ±ĻßBD½»Ļ߶ĪACÓŚµćE£¬”÷CDEµÄĆ껿ĪŖ![]() £¬”÷BCEµÄĆ껿ĪŖ
£¬”÷BCEµÄĆ껿ĪŖ![]() £¬Ēó
£¬Ēó![]() µÄ×ī“óÖµ£»
µÄ×ī“óÖµ£»
¢Ś¹żµćD×÷DF”ĶAC£¬“¹×ćĪŖµćF£¬Į¬½ÓCD£¬ŹĒ·ń“ęŌŚµćD£¬Ź¹µĆ”÷CDFÖŠµÄijøö½ĒĒ”ŗƵČÓŚ”ĻBACµÄ2±¶£æČō“ęŌŚ£¬ĒóµćDµÄŗį×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©¢Ł
£»£Ø2£©¢Ł![]() £»¢Ś©2»ņ
£»¢Ś©2»ņ![]() £®
£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾ŻĢāŅāµĆµ½A£Ø©4£¬0£©£¬C£Ø0£¬2£©“śČė![]() £¬ÓŚŹĒµĆµ½½įĀŪ£»
£¬ÓŚŹĒµĆµ½½įĀŪ£»
£Ø2£©¢ŁČēĶ¼£¬Įīy=0£¬½ā·½³ĢµĆµ½x1=©4£¬x2=1£¬ĒóµĆB£Ø1£¬0£©£¬¹żD×÷DM”ĶxÖįÓŚM£¬¹żB×÷BN”ĶxÖį½»ÓŚACÓŚN£¬øł¾ŻĻąĖĘČż½ĒŠĪµÄŠŌÖŹ¼“æɵƵ½½įĀŪ£»
¢Śøł¾Ż¹“¹É¶ØĄķµÄÄę¶ØĄķµĆµ½”÷ABCŹĒŅŌ”ĻACBĪŖÖ±½ĒµÄÖ±½ĒČż½ĒŠĪ£¬Č”ABµÄÖŠµćP£¬ĒóµĆP£Ø![]() £¬0£©£¬µĆµ½PA=PC=PB=
£¬0£©£¬µĆµ½PA=PC=PB=![]() £¬¹ż×÷xÖįµÄĘ½ŠŠĻß½»yÖįÓŚR£¬½»ACµÄŃÓĻßÓŚG£¬ĒéæöŅ»£ŗČēĶ¼£¬”ĻDCF=2”ĻBAC=”ĻDGC+”ĻCDG£¬Ēéæö¶ž£¬”ĻFDC=2”ĻBAC£¬½āÖ±½ĒČż½ĒŠĪ¼“æɵƵ½½įĀŪ£®
£¬¹ż×÷xÖįµÄĘ½ŠŠĻß½»yÖįÓŚR£¬½»ACµÄŃÓĻßÓŚG£¬ĒéæöŅ»£ŗČēĶ¼£¬”ĻDCF=2”ĻBAC=”ĻDGC+”ĻCDG£¬Ēéæö¶ž£¬”ĻFDC=2”ĻBAC£¬½āÖ±½ĒČż½ĒŠĪ¼“æɵƵ½½įĀŪ£®
ŹŌĢā½āĪö£ŗ£Ø1£©øł¾ŻĢāŅāµĆA£Ø©4£¬0£©£¬C£Ø0£¬2£©£¬”ßÅ×ĪļĻß![]() ¾¹żA”¢CĮ½µć£¬”ą
¾¹żA”¢CĮ½µć£¬”ą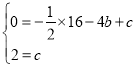 £¬”ą
£¬”ą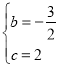 £¬”ą
£¬”ą![]() £»
£»
£Ø2£©¢ŁČēĶ¼£¬Įīy=0£¬”ą![]() £¬”ąx1=©4£¬x2=1£¬”ąB£Ø1£¬0£©£¬¹żD×÷DM”ĶxÖįÓŚM£¬¹żB×÷BN”ĶxÖį½»ÓŚACÓŚN£¬”ąDM”ĪBN£¬”ą”÷DME”×”÷BNE£¬”ą
£¬”ąx1=©4£¬x2=1£¬”ąB£Ø1£¬0£©£¬¹żD×÷DM”ĶxÖįÓŚM£¬¹żB×÷BN”ĶxÖį½»ÓŚACÓŚN£¬”ąDM”ĪBN£¬”ą”÷DME”×”÷BNE£¬”ą![]() =
=![]() =
=![]() £¬ÉčD£Øa£¬
£¬ÉčD£Øa£¬ ![]() £©£¬”ąM£Øa£¬
£©£¬”ąM£Øa£¬![]() £©£¬”ßB£Ø1.0£©£¬”ąN£Ø1£¬
£©£¬”ßB£Ø1.0£©£¬”ąN£Ø1£¬![]() £©£¬”ą
£©£¬”ą![]() =
=![]() =
=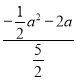 =
=![]() £»”ąµ±a=-2Ź±£¬
£»”ąµ±a=-2Ź±£¬![]() µÄ×ī“óÖµŹĒ
µÄ×ī“óÖµŹĒ![]() £»
£»
¢Ś”ßA£Ø©4£¬0£©£¬B£Ø1£¬0£©£¬C£Ø0£¬2£©£¬”ąAC=![]() £¬BC=
£¬BC=![]() £¬AB=5£¬”ąAC2+BC2=AB2£¬”ą”÷ABCŹĒŅŌ”ĻACBĪŖÖ±½ĒµÄÖ±½ĒČż½ĒŠĪ£¬Č”ABµÄÖŠµćP£¬”ąP£Ø
£¬AB=5£¬”ąAC2+BC2=AB2£¬”ą”÷ABCŹĒŅŌ”ĻACBĪŖÖ±½ĒµÄÖ±½ĒČż½ĒŠĪ£¬Č”ABµÄÖŠµćP£¬”ąP£Ø![]() £¬0£©£¬”ąPA=PC=PB=
£¬0£©£¬”ąPA=PC=PB=![]() £¬”ą”ĻCPO=2”ĻBAC£¬”ątan”ĻCPO=tan£Ø2”ĻBAC£©=
£¬”ą”ĻCPO=2”ĻBAC£¬”ątan”ĻCPO=tan£Ø2”ĻBAC£©=![]() £¬¹ż×÷xÖįµÄĘ½ŠŠĻß½»yÖįÓŚR£¬½»ACµÄŃÓ³¤ĻßÓŚG£®·ÖĮ½ÖÖĒéæö£ŗ
£¬¹ż×÷xÖįµÄĘ½ŠŠĻß½»yÖįÓŚR£¬½»ACµÄŃÓ³¤ĻßÓŚG£®·ÖĮ½ÖÖĒéæö£ŗ
ĒéæöŅ»£ŗČēĶ¼£¬”ą”ĻDCF=2”ĻBAC=”ĻDGC+”ĻCDG£¬”ą”ĻCDG=”ĻBAC£¬”ątan”ĻCDG=tan”ĻBAC=![]() £¬¼“
£¬¼“![]() £¬ĮīD£Øa£¬
£¬ĮīD£Øa£¬![]() £©£¬”ąDR=©a£¬RC=
£©£¬”ąDR=©a£¬RC=![]() £¬”ą
£¬”ą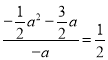 £¬”ąa1=0£ØÉįČ„£©£¬a2=©2£¬”ąxD=©2£®
£¬”ąa1=0£ØÉįČ„£©£¬a2=©2£¬”ąxD=©2£®
Ēéæö¶ž£¬”ą”ĻFDC=2”ĻBAC£¬”ątan”ĻFDC=![]() £¬ÉčFC=4k£¬”ąDF=3k£¬DC=5k£¬”ßtan”ĻDGC=
£¬ÉčFC=4k£¬”ąDF=3k£¬DC=5k£¬”ßtan”ĻDGC=![]() =
=![]() £¬”ąFG=6k£¬”ąCG=2k£¬DG=
£¬”ąFG=6k£¬”ąCG=2k£¬DG=![]() k£¬”ą
k£¬”ą
”ąRC=![]() k£¬RG=
k£¬RG=![]() k£¬DR=
k£¬DR=![]() k©
k©![]() k=
k=![]() k£¬”ą
k£¬”ą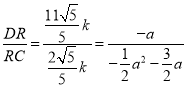 £¬”ąa1=0£ØÉįČ„£©£¬a2=
£¬”ąa1=0£ØÉįČ„£©£¬a2=![]() £®
£®
×ŪÉĻĖłŹö£ŗµćDµÄŗį×ų±źĪŖ©2»ņ![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»“ĪŗÆŹży=3x+2µÄĶ¼Ļó²»¾¹ż£Ø £©
A.µŚŅ»ĻóĻŽ
B.µŚ¶žĻóĻŽ
C.µŚČżĻóĻŽ
D.µŚĖÄĻóĻŽ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬![]() Óė
Óė![]() ĻąĒŠÓŚµć
ĻąĒŠÓŚµć![]() £¬
£¬![]() ĪŖ
ĪŖ![]() µÄĻŅ£¬
µÄĻŅ£¬![]() £¬
£¬![]() Óė
Óė![]() Ļą½»ÓŚµć
Ļą½»ÓŚµć![]() £»
£»
£Ø1£©ĒóÖ¤£ŗ![]() £»
£»
£Ø2£©Čō![]() £¬
£¬![]() £¬ĒóĻ߶Ī
£¬ĒóĻ߶Ī![]() µÄ³¤£®
µÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬½«Å×ĪļĻßy=£Øx©1£©2ĻČĻņÉĻĘ½ŅĘ2øöµ„Ī»³¤¶Č£¬ŌŁĻņÓŅĘ½ŅĘ3øöµ„Ī»³¤¶Č£¬µĆµ½µÄÅ×ĪļĻߵĽāĪöŹ½ŹĒ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖyŹĒx µÄŗÆŹż£¬×Ō±äĮæxµÄȔֵ·¶Ī§ŹĒx >0£¬ĻĀ±ķŹĒyÓėx µÄ¼ø×é¶ŌÓ¦Öµ.
x | ”¤”¤”¤ | 1 | 2 | 3 | 5 | 7 | 9 | ”¤”¤”¤ |
y | ”¤”¤”¤ | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ”¤”¤”¤ |
Š”ĢŚøł¾ŻŃ§Ļ°Ņ»“ĪŗÆŹżµÄ¾Ń飬ĄūÓĆÉĻŹö±ķøńĖł·“Ó³³öµÄyÓėxÖ®¼äµÄ±ä»Æ¹ęĀÉ£¬¶ŌøĆŗÆŹżµÄĶ¼ĻóÓėŠŌÖŹ½ųŠŠĮĖĢ½¾æ.
ĻĀĆęŹĒŠ”ĢŚµÄĢ½¾æ¹ż³Ģ£¬Ēė²¹³äĶźÕū£ŗ
£Ø1£©ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµ ![]() ÖŠ£¬Ćč³öĮĖŅŌÉĻ±ķÖŠø÷¶Ō¶ŌÓ¦ÖµĪŖ×ų±źµÄµć.øł¾ŻĆč³öµÄµć£¬»³öøĆŗÆŹżµÄĶ¼Ļó;
ÖŠ£¬Ćč³öĮĖŅŌÉĻ±ķÖŠø÷¶Ō¶ŌÓ¦ÖµĪŖ×ų±źµÄµć.øł¾ŻĆč³öµÄµć£¬»³öøĆŗÆŹżµÄĶ¼Ļó;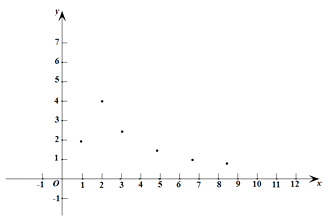
£Ø2£©øł¾Ż»³öµÄŗÆŹżĶ¼Ļ󣬊“³ö£ŗ
¢Łx=4¶ŌÓ¦µÄŗÆŹżÖµyŌ¼ĪŖ£»
¢ŚøĆŗÆŹżµÄŅ»ĢõŠŌÖŹ£ŗ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ±ą×«×ę¹śµÄÓÅŠć“«Ķ³ĪĻƣ¬Ä³Š£×éÖÆĮĖŅ»“Ī”°Ź«“Ź“ó»į”±£¬Š”Ć÷ŗĶŠ”ĄöĶ¬Ź±²Ī¼Ó£¬ĘäÖŠ£¬ÓŠŅ»µĄ±Ų“šĢāŹĒ£ŗ“ÓČēĶ¼ĖłŹ¾µÄ¾Å¹¬øń֊єȔĘßøö×Ö×é³ÉŅ»¾äĢĘŹ«£¬Ęä“š°øĪŖ”°É½ÖŲĖ®ø“ŅÉĪŽĀ·”±£®
£Ø1£©Š”Ć÷»Ų“šøĆĪŹĢāŹ±£¬¶ŌµŚ¶žøö×ÖŹĒŃ””°ÖŲ”±»¹ŹĒŃ””°Ēī”±ÄŃŅŌ¾ńŌń£¬ČōĖ껜єŌńĘäÖŠŅ»øö£¬ŌņŠ”Ć÷»Ų“šÕżČ·µÄøÅĀŹŹĒ £»
£Ø2£©Š”Ąö»Ų“šøĆĪŹĢāŹ±£¬¶ŌµŚ¶žøö×ÖŹĒŃ””°ÖŲ”±»¹ŹĒŃ””°Ēī”±”¢µŚĖÄøö×ÖŹĒŃ””°ø»”±»¹ŹĒŃ””°ø“”±¶¼ÄŃŅŌ¾ńŌń£¬Čō·Ö±šĖ껜єŌń£¬ĒėÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·ØĒ󊔥ö»Ų“šÕżČ·µÄøÅĀŹ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬”÷ABCµÄ¶„µć·Ö±šĪŖA£Ø-4£¬ 5£©£¬B£Ø©3£¬ 2£©£¬C£Ø4£¬-1£©£®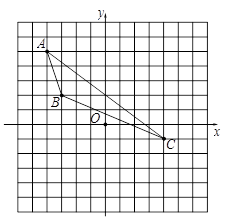
£Ø1£©×÷³ö”÷ABC¹ŲÓŚxÖį¶Ō³ĘµÄĶ¼ŠĪ”÷A1B1C1£»
£Ø2£©Š“³öA1”¢B1”¢C1µÄ×ų±ź£»
£Ø3£©ČōAC=10£¬Ēó”÷ABCµÄAC±ßÉĻµÄøߣ®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬Å×ĪļĻß
ÖŠ£¬Å×ĪļĻß![]() µÄæŖæŚĻņÉĻ£¬ĒŅ¾¹żµć
µÄæŖæŚĻņÉĻ£¬ĒŅ¾¹żµć![]() .
.
£Ø1£©Čō“ĖÅ×ĪļĻß¾¹żµć![]() £¬ĒŅÓė
£¬ĒŅÓė![]() ÖįĻą½»ÓŚµć
ÖįĻą½»ÓŚµć![]() .
.
¢ŁĢīæÕ£ŗ![]() £ØÓĆŗ¬
£ØÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾£©£»
µÄ“śŹżŹ½±ķŹ¾£©£»
¢Śµ±![]() µÄÖµ×īŠ”Ź±£¬ĒóÅ×ĪļĻߵĽāĪöŹ½£»
µÄÖµ×īŠ”Ź±£¬ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©Čō![]() £¬µ±
£¬µ±![]() £¬Å×ĪļĻßÉĻµÄµćµ½
£¬Å×ĪļĻßÉĻµÄµćµ½![]() Öį¾ąĄėµÄ×ī“óÖµĪŖ3Ź±£¬Ēó
Öį¾ąĄėµÄ×ī“óÖµĪŖ3Ź±£¬Ēó![]() µÄÖµ.
µÄÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
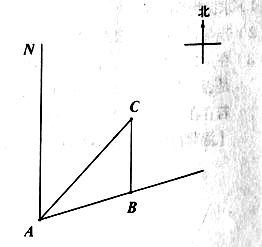
”¾ĢāÄæ”æČēĶ¼£¬Ņ»ĖŅ“¬ŅŌĆ抔Ź±30ŗ£ĄļµÄĖŁ¶ČĻņ±±Ę«¶«75”ć·½Ļņŗ½ŠŠ£¬ŌŚµć![]() “¦²āµĆĀėĶ·
“¦²āµĆĀėĶ·![]() µÄ“¬µÄ¶«±±·½Ļņ£¬ŗ½ŠŠ40·ÖÖÓŗ󵽓ļ
µÄ“¬µÄ¶«±±·½Ļņ£¬ŗ½ŠŠ40·ÖÖÓŗ󵽓ļ![]() “¦£¬ÕāŹ±ĀėĶ·
“¦£¬ÕāŹ±ĀėĶ·![]() Ē”ŗĆŌŚ“¬µÄÕż±±·½Ļņ£¬ŌŚ“¬²»øıäŗ½ĻņµÄĒéæöĻĀ£¬Ēó³ö“¬ŌŚŗ½ŠŠ¹ż³ĢÖŠÓėĀėĶ·
Ē”ŗĆŌŚ“¬µÄÕż±±·½Ļņ£¬ŌŚ“¬²»øıäŗ½ĻņµÄĒéæöĻĀ£¬Ēó³ö“¬ŌŚŗ½ŠŠ¹ż³ĢÖŠÓėĀėĶ·![]() µÄ×ī½ü¾ąĄė.£Ø½į¹ū¾«Č·µÄ0£®1ŗ£Ąļ£¬²Īæ¼Źż¾Ż
µÄ×ī½ü¾ąĄė.£Ø½į¹ū¾«Č·µÄ0£®1ŗ£Ąļ£¬²Īæ¼Źż¾Ż![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com