练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，每个小正方形的边长均为1.求四边形ABCD的面积和周长(精确到0.1).

    【答案】四边形ABCD的周长是8，四边形ABCD的面积是17.5.

    【解析】

    首先根据勾股定理求得AB、BC、CD、DA、AC的长，根据勾股定理的逆定理判断∠ABC和∠ACD是直角，即可求解．

    根据勾股定理得到:

    AD==，

    AB==，

    CD==5;

    BC==，

    ∴四边形ABCD的周长是

    AB+BC+CD+AD=++5+≈18.8.

    连接AC，BD，则AC==5.

    ∵(2)2+()2=52，52+52=(5)2，

    ∴AB2+BC2=AC2，AC2+CD2=AD2.

    ∴∠ABC和∠ACD是直角.

    ∴四边形ABCD的面积=直角△ABC的面积+直角△ACD的面积=BC·AB+AC·CD=17.5.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣ x2﹣ x+ 与x轴交于A，B两点（A点在B点的左侧），与y轴交于点C，已知点D（0，﹣ ）．

    （1）求直线AC的解析式；
    （2）如图1，P为直线AC上方抛物线上的一动点，当△PBD面积最大时，过P作PQ⊥x轴于点Q，M为抛物线对称轴上的一动点，过M作y轴的垂线，垂足为点N，连接PM，NQ，求PM+MN+NQ的最小值；
    （3）在（2）问的条件下，将得到的△PBQ沿PB翻折得到△PBQ′，将△BPQ′沿直线BD平移，记平移中的△PBQ′为△P′B′Q″，在平移过程中，设直线P′B′与x轴交于点E．则是否存在这样的点E，使得△B′EQ″为等腰三角形？若存在，求此时OE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC中，BC=a，AC=b，AB=c，若∠C=90°，如图（1），根据勾股定理，则a2+b2=c2，若△ABC不是直角三角形，如图（2）和图（3），请你类比勾股定理，试猜想a2+b2与c2的关系，并证明你的结论.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，O为坐标原点，四边形OACB是菱形，OB在x轴的正半轴上，sin∠AOB= ，反比例函数y= 在第一象限内的图象经过点A，与BC交于点F，则△AOF的面积等于 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是一块直角三角形的绿地，量得直角边BC为6cm，AC为8cm，现在要将原绿地扩充后成等腰三角形，且扩充的部分是以AC为直角边的直角三角形，求扩充后的等腰三角形绿地的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，半圆O的直径BC=7，延长CB到A，割线AED交半圆于点E，D，且AE=ED=3，则AB的长为（ ）

    A.
    B.2
    C.
    D.9

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB．添加一个条件，不能使四边形DBCE成为矩形的是（ ）

    （A）AB=BE （B）BE⊥DC （C）∠ADB=90° （D）CE⊥DE

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线l：y= x，过点M（2，0）作x轴的垂线交直线l于点N，过点N作直线l的垂线交x轴于点M1；过点M1作x轴的垂线交直线l于N1 ， 过点N1作直线l的垂线交x轴于点M2 ， …；按此作法继续下去，则点M8坐标为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

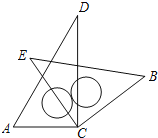
    【题目】小明将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起，当∠ACE＜180°且点E在直线AC的上方时，他发现若∠ACE＝_____，则三角板BCE有一条边与斜边AD平行．（写出所有可能情况）

    查看答案和解析>>

    同步练习册答案