
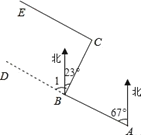
【题目】如图,某工程队从A点出发,沿北偏西67°方向修一条公路AD,在BD路段出现塌陷区,就改变方向,由B点沿北偏东23°的方向继续修建BC段,到达C点又改变方向,从C点继续修建CE段,∠ECB应为多少度,可使所修路段CE∥AB?试说明理由.此时CE与BC有怎样的位置关系?
以下是小刚不完整的解答,请帮他补充完整.
解:由已知平行,得∠1=∠A=67°(两直线平行, )
∴∠CBD=23°+67°= °,
当∠ECB+∠CBD= °时,
可得CE∥AB.( )
所以∠ECB= °
此时CE⊥BC.( )
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
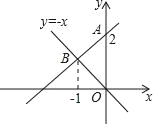
【题目】如图,一次函数图象经过点A(0,2),且与正比例函数y=﹣x的图象交于点B,B点的横坐标是﹣1.
(1)求该一次函数的解析式:
(2)求一次函数图象、正比例函数图象与x轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016新疆)如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 (小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正三角形ABC的边长为3+![]() .
.
(1)如图,正方形EFPN的顶点E,F在边AB上,顶点N在边AC上,在正三角形ABC及其内部,以点A为位似中心,作正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不要求写作法);
(2)求(1)中作出的正方形E′F′P′N′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,设购进A型节能灯m只.
①请用含m的代数式表示总费用;
②请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com