
 ij��ѧ��ȤС���ͬѧ��һ��̽���з��֣���ƽ��ֱ������ϵ��������A��x1��y1����B��x2��y2�������߶�AB���е�C������Ϊ��$\frac{{{x_1}+{x_2}}}{2}��\frac{{{y_1}+{y_2}}}{2}$����������һ�������ۣ������ؽ�����λ�ߺ�һ�κ�����֪ʶ֤������һ���ۣ�����ʹ�øý��۽���������⣮
ij��ѧ��ȤС���ͬѧ��һ��̽���з��֣���ƽ��ֱ������ϵ��������A��x1��y1����B��x2��y2�������߶�AB���е�C������Ϊ��$\frac{{{x_1}+{x_2}}}{2}��\frac{{{y_1}+{y_2}}}{2}$����������һ�������ۣ������ؽ�����λ�ߺ�һ�κ�����֪ʶ֤������һ���ۣ�����ʹ�øý��۽���������⣮���� ��1��ֱ�Ӹ����е����깫ʽ���ɵó����ۣ�
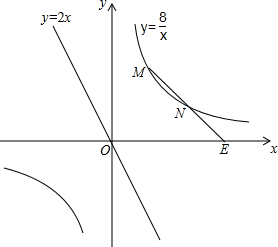
��2����M��x��$\frac{8}{x}$���������е����깫ʽ��x��ʾ��N�����꣬�ٸ��ݵ�N��˫�����Ͽɵó�x��ֵ�������ó�M��N��������ꣻ
��3����P��a��0����Q��x��-2x�����ٷ�MN��ƽ���ı��εĶԽ�����MP��ƽ���ı��εĶԽ�����������������ۣ�
��� �⣺��1����D��5��2����E��-1��-4����
���߶�DE���е�F������Ϊ��$\frac{5-1}{2}$��$\frac{2-4}{2}$������F��2��-1����
�ʴ�Ϊ��2��-1����
��2���ߵ�M��˫����y=$\frac{8}{x}$�ϣ�
����M��x��$\frac{8}{x}$����
�ߵ�K������Ϊ��6��0������N���߶�MK���е㣬
��N��$\frac{x+6}{2}$��$\frac{4}{x}$����
�ߵ�NҲ��˫����y=$\frac{8}{x}$�ϣ�
��$\frac{4}{x}$=$\frac{8}{\frac{x+6}{2}}$�����x=2��
��M��2��4����N��4��2����
�ʴ�Ϊ����2��4������4��2����
��3����P��a��0����Q��x��-2x����
��MN��ƽ���ı��εĶԽ���ʱ��
��M��2��4����N��4��2����
��2+4=a+x��4+2=-2x�����x=-3��a=9��
��P��9��0����Q��-3��6����
��MP��ƽ���ı��εĶԽ���ʱ��
2+a=4+x��4=-2x+2�����x=-1��a=1��
��P��1��0����Q��-1��2����
��NPΪ�Խ���ʱ����֪P��-1��0����Q��1��-2��
������������P�͵�Q������ΪP��9��0����Q��-3��6����P��1��0����Q��-1��2����-1��0����Q��1��-2����
���� ���⿼����Ƿ����������ۺ��⣬�漰������������ͼ���ϵ�������ص㼰ƽ���ı��ε��ж���֪ʶ���ڽ��3��ʱҪע����з������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
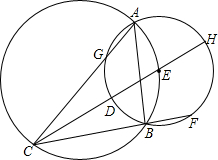 ��ͼ����E��Բ���ڡ�O�ϣ���E����O��A��B���㣬��O����CE����ֱ�߽���E�ڵ�D��H��CB���ӳ��߽���E�ڵ�F��
��ͼ����E��Բ���ڡ�O�ϣ���E����O��A��B���㣬��O����CE����ֱ�߽���E�ڵ�D��H��CB���ӳ��߽���E�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
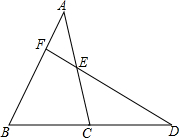 �ڡ�ABC�У���D��BC���ӳ����ϣ�E��AC���е㣬DE���ӳ��߽�AB�ڵ�F��
�ڡ�ABC�У���D��BC���ӳ����ϣ�E��AC���е㣬DE���ӳ��߽�AB�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
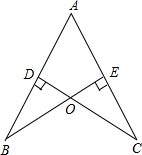 ��ͼ��AB=AC��CD��AB�ڵ�D��BE��AC�ڵ�E��BE��CD�ཻ�ڵ�O��
��ͼ��AB=AC��CD��AB�ڵ�D��BE��AC�ڵ�E��BE��CD�ཻ�ڵ�O���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
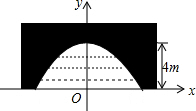 ��ͼ��һ���Ź��ŵĽ���ͼ�����Ŷ�����������״������Ϊ10m���Ŷ���ˮ���������Ϊ4m�������ŵĺ���������ͼ��ʾ��ƽ��ֱ������ϵ�У�
��ͼ��һ���Ź��ŵĽ���ͼ�����Ŷ�����������״������Ϊ10m���Ŷ���ˮ���������Ϊ4m�������ŵĺ���������ͼ��ʾ��ƽ��ֱ������ϵ�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
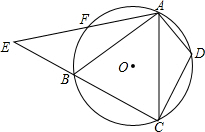 ��ͼ����ABC�ڽ��ڡ�O��D��F�ֱ���$\widehat{AC}$��$\widehat{AB}$�ϵĵ㣬$\widehat{BF}$=$\widehat{DA}$������AF���ӳ���CB���ӳ����ڵ�E������AD��CD����֤����CDA�ס�ABE��
��ͼ����ABC�ڽ��ڡ�O��D��F�ֱ���$\widehat{AC}$��$\widehat{AB}$�ϵĵ㣬$\widehat{BF}$=$\widehat{DA}$������AF���ӳ���CB���ӳ����ڵ�E������AD��CD����֤����CDA�ס�ABE���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com