
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
【答案】(1)F(243)=9,F(617)=14;(2)![]() .
.
【解析】
试题分析:(1)根据F(n)的定义式,分别将n=243和n=617代入F(n)中,即可求出结论;
(2)由s=100x+32、t=150+y结合F(s)+F(t)=18,即可得出关于x、y的二元一次方程,解之即可得出x、y的值,再根据“相异数”的定义结合F(n)的定义式,即可求出F(s)、F(t)的值,将其代入k=![]() 中,找出最大值即可.
中,找出最大值即可.
试题解析:(1)F(243)=(423+342+234)÷111=9;
F(617)=(167+716+671)÷111=14.
(2)∵s,t都是“相异数”,s=100x+32,t=150+y,∴F(s)=(302+10x+230+x+100x+23)÷111=x+5,F(t)=(510+y+100y+51+105+10y)÷111=y+6.
∵F(t)+F(s)=18,∴x+5+y+6=x+y+11=18,∴x+y=7.
∵1≤x≤9,1≤y≤9,且x,y都是正整数,∴![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() .
.
∵s是“相异数”,∴x≠2,x≠3.
∵t是“相异数”,∴y≠1,y≠5,∴![]() 或
或![]() 或
或![]() ,∴
,∴![]() 或
或![]() 或
或![]() ,∴k=
,∴k=![]() =
=![]() 或k=
或k=![]() =1或k=
=1或k=![]() =
=![]() ,∴k的最大值为
,∴k的最大值为![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
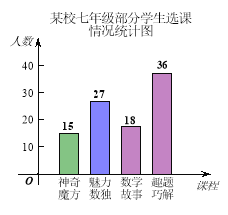
【题目】(本题8分)为培养学生数学学习兴趣,某校七年级准备开设“神奇魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课(每位学生必须且只选其中一门).
(1)学校对七年级部分学生进行选课调查,得到如图所示的统计图,根据该统计图,请估计该校七年级480名学生选“数学故事”的人数。
(2)学校将选“数学故事”的学生分成人数相等的A,B,C三个班,小聪、小慧都选择了“数学故事”,已知小聪不在A班,求他和小慧被分到同一个班的概率.(要求列表或画树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C与某建筑物底端B相距306米(点C与点B在同一水平面上),某同学从点C出发,沿同一剖面的斜坡CD行走195米至坡顶D处,斜坡CD的坡度(或坡比)i=1:2.4,在D处测得该建筑物顶端A的俯视角为20°,则建筑物AB的高度约为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)( )
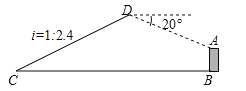
A.29.1米 B.31.9米 C.45.9米 D.95.9米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4 , …均为等边三角形,若OA1=2,则△A5B5A6的边长为 . 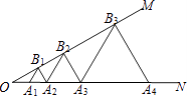
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究与应用: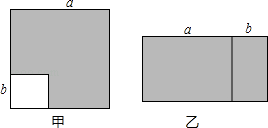
(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分面积是(写成两数平方差的形式)
(2)小颖将阴影部分裁下来,重新拼成一个长方形,如图乙,则长方形的长是 , 宽是 , 面积是(写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到公式(用式子表达)
(4)运用你所得到的公式计算:10.3×9.7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是交警在某个路口统计的某时段来往车辆的车速情况.(单位:千米/时)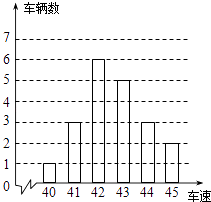
(1)车速的众数是多少?
(2)计算这些车辆的平均数度;
(3)车速的中位数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(﹣2,1)的对应点为A′(3,1),点B的对应点为B′(4,0),则点B的坐标为( )
A.(9,0)
B.(﹣1,0)
C.(3,﹣1)
D.(﹣3,﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com