
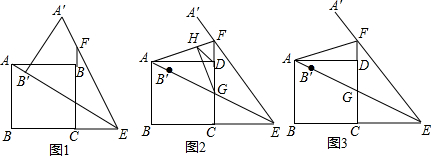
分析 (1)根据DF=FG-DG,求出DG、DG的长即解决问题.
(2)如图2中,作AM⊥EF于M,HN⊥CF于N,HJ⊥AD于J.首先证明∠HAG=45°,四边形HJDN是正方形,设边长为b,正方形ABC的边长为2a,则DG=a,AJ=GN=a+b=2a-b,推出a=2b,求出CE、DH用b表示,即可解决问题.
(3)结论:EF2=CE2+$\frac{8}{5}$AF2.由(2)可知,tan∠HGN=tan∠FAD=$\frac{HN}{NG}$=$\frac{b}{3b}$=$\frac{1}{3}$,求出DF、AF的长,以及CF与AF的关系,在Rt△EFC中,根据EF2=EC2+CF2,即可解决问题.
解答 (1)解:如图1中,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=1,∠B=∠BCD=∠DCE=90°,
∵∠AEB=∠A′EA=30°,
∴BE=$\sqrt{3}$AB=$\sqrt{3}$,EC=BE-BC=$\sqrt{3}-1$,
∴CG=EC•tan30°=1-$\frac{\sqrt{3}}{3}$,GE=2GC=2-$\frac{2\sqrt{3}}{3}$,DG=CD-CG=$\frac{\sqrt{3}}{3}$,
∵∠CGE=∠A′EA+∠GFE=60°,
∴∠GFE=∠GEF=30°,
∴FG=GE=2-$\frac{2\sqrt{3}}{3}$,
∴DF=GF-DG=2-$\frac{2\sqrt{3}}{3}$-$\frac{\sqrt{3}}{3}$=2-$\sqrt{3}$.
(2)证明:如图2中,作AM⊥EF于M,HN⊥CF于N,HJ⊥AD于J.
∵AD∥BE,
∴∠DAG=∠BEG=∠AEF,
∵AB⊥BE,AM⊥EM,
∴AB=AM=AD,
在Rt△AFM和Rt△AFD中,
$\left\{\begin{array}{l}{AF=AF}\\{AM=AD}\end{array}\right.$,
∴Rt△AFM≌Rt△AFD,
∴∠MAF=∠FAD,
∵∠MAE+∠MEA=90°,
∴2∠FAD+2∠DAG=90°,
∴∠FAD+∠DAG=45°,
∴∠HAG=45°,
∵GH⊥AF,
∴∠HAG=∠HGA=45°,
∴AH=GH,
∵∠FAD+∠AFD=90°∠HGF+∠HFG=90°,
∴∠HAJ=∠HGN,
∴△AHJ≌△GHN,
∴JH=HN,
∵四边形HJDN是矩形,
∴四边形HJDN是正方形,设边长为b,正方形ABC的边长为2a,则DG=a,AJ=GN=a+b=2a-b,
∴a=2b,
∵AD∥CE,
∴$\frac{AD}{CE}$=$\frac{DG}{GC}$,
∵DG=GC,
∴AD=CE=2a=4b,
∵DH=$\sqrt{2}$b,
∴b=$\frac{\sqrt{2}}{2}$DH,
∴CE=4•$\frac{\sqrt{2}}{2}$DH=2$\sqrt{2}$DH.
(3)解:结论:EF2=CE2+$\frac{8}{5}$AF2.理由如下,
如图3中,由(2)可知,tan∠HGN=tan∠FAD=$\frac{HN}{NG}$=$\frac{b}{3b}$=$\frac{1}{3}$,
∴DF=$\frac{1}{3}$AD=$\frac{4}{3}$b,
AF=$\sqrt{A{D}^{2}+D{F}^{2}}$=$\sqrt{(4b)^{2}+(\frac{4}{3}b)^{2}}$=$\frac{4}{3}$$\sqrt{10}$b,
∴b=$\frac{3AF}{4\sqrt{10}}$,
∵CF=DF+CD=4b+$\frac{4}{3}$b=$\frac{16}{3}$b=$\frac{4}{\sqrt{10}}$AF,
在Rt△EFC中,∵EF2=EC2+CF2,
∴EF2=CE2+($\frac{4}{\sqrt{10}}AF$)2,
∴EF2=CE2+$\frac{8}{5}$AF2.
点评 本题考查正方形的性质、全等三角形的判定和性质、四点共圆等知识,解题的关键是添加辅助线构造全等三角形,学会利用参数,构建方程解决问题.属于中考常考题型.


科目:初中数学 来源: 题型:填空题
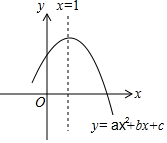 如图是二次函数y=ax2+bx+c的图象,图象过点A(3,0),对称轴为直线x=1,给出以下结论:①abc<0;②b2-4ac>0;③a-b+c=0;④若B(m2+1,y1)、C(m2+2,y2)为函数图象上的两点,则y1<y2;⑤当-1≤x≤3时,y≥0.其中正确的结论是①②③⑤.(填写正确结论的序号)
如图是二次函数y=ax2+bx+c的图象,图象过点A(3,0),对称轴为直线x=1,给出以下结论:①abc<0;②b2-4ac>0;③a-b+c=0;④若B(m2+1,y1)、C(m2+2,y2)为函数图象上的两点,则y1<y2;⑤当-1≤x≤3时,y≥0.其中正确的结论是①②③⑤.(填写正确结论的序号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
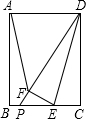 如图,在矩形ABCD中,AB=6,BC=4,点E是边BC上一动点,把△DCE沿DE折叠得△DFE,射线DF交直线CB于点P,当△AFD为等腰三角形时,DP的长为$\frac{9}{2}$$\sqrt{2}$或$\frac{24}{7}\sqrt{7}$.
如图,在矩形ABCD中,AB=6,BC=4,点E是边BC上一动点,把△DCE沿DE折叠得△DFE,射线DF交直线CB于点P,当△AFD为等腰三角形时,DP的长为$\frac{9}{2}$$\sqrt{2}$或$\frac{24}{7}\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
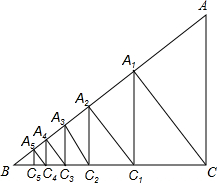 如图,已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C2作C2A2⊥AB,垂足为A2,再过A3作A3C3⊥BC,垂足为C3,…,这样一直做下去,得到了一组线段CA1,A1C1,C2A2,…,则$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{5}{4}$.
如图,已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C2作C2A2⊥AB,垂足为A2,再过A3作A3C3⊥BC,垂足为C3,…,这样一直做下去,得到了一组线段CA1,A1C1,C2A2,…,则$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{5}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
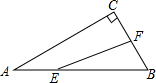 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC的中点.若动点E以2cm/s的速度从A点出发,沿着A→B→A的方向运动,设运动时间为t(s)(0≤t≤3),连接EF,当t为1s或3s或$\frac{7}{4}$s或$\frac{9}{4}$s时,△BEF是直角三角形.
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC的中点.若动点E以2cm/s的速度从A点出发,沿着A→B→A的方向运动,设运动时间为t(s)(0≤t≤3),连接EF,当t为1s或3s或$\frac{7}{4}$s或$\frac{9}{4}$s时,△BEF是直角三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com