
分析 根据分式的运算法则即可求出答案.
解答 解:(1)原式=$\frac{a-b}{a+b}$•$\frac{{a}^{2}({a}^{2}-{b}^{2})}{a(a-b)}$
=$\frac{a-b}{a+b}$•$\frac{{a}^{2}(a-b)(a+b)}{a(a-b)}$
=a2-ab
(2)原式=$\frac{(2x-y)^{2}}{2x+y}$×$\frac{1}{(2x+y)(2x-y)}$
=$\frac{2x-y}{(2x+y)^{2}}$
(3)原式=$\frac{{y}^{3}}{{x}^{3}}$•$\frac{1}{2y}$
=$\frac{{y}^{2}}{{x}^{3}}$
点评 本题考查分式的乘除法,解题的关键是熟练运用分式的运算法则的,本题属于基础题型.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
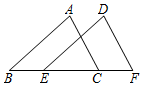 如图,在△ABC和△DEF中,已知∠B=∠DEF,AB=ED,加上该条件后仍无法证明△ABC≌△DEF的是( )
如图,在△ABC和△DEF中,已知∠B=∠DEF,AB=ED,加上该条件后仍无法证明△ABC≌△DEF的是( )| A. | AC=DF | B. | BE=CF | C. | AC∥DF | D. | ∠A=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30个 | B. | 80个 | C. | 90个 | D. | 120个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com